數學公式集錦
1. 在坐標平面上,兩坐標軸(x軸與y軸)將平面分成四個部分(不含x軸與y軸),右上角部分稱為第一象限;左上角部分稱為第二象限;左下角部分稱為第三象限;右下角部分稱為第四象限。
2. 數線上兩點P(a)、Q(b),則P、Q兩點的距離為![]() 。
。
3. 設平面上兩點P(x1,y1)、Q(x2,y2),則P、Q兩點的距離為
![]() 。
。
4. 設P1(x1,y1)、P2(x2,y2)、P(x,y)為同一直線上相異三點,m、n為正數,且![]() ,若P在線段
,若P在線段![]() 上,則稱P為
上,則稱P為![]() 之內分點,且
之內分點,且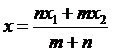 ,
,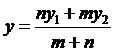 。
。
5. 設坐標平面上相異兩點P1(x1,y1)、P2(x2,y2),且![]() 的中點坐標為P(x,y),則
的中點坐標為P(x,y),則 ,
,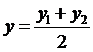 。
。
6. 已知△ABC的三頂點坐標為A(x1,y1)、B(x2,y2)、C(x3,y3),則△ABC的重心坐標為
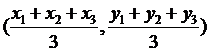 。
。
1. 設平面上有一直線L,且P1(x1,y1)、P2(x2,y2)為直線L上的兩個相異點。
(1) 當x1
¹
x2時,直線L的斜率為 。
。
(2) 當x1 = x2時,直線L的斜率m不存在,表示直線L垂直於x軸。
2. 設兩相異直線L1與L2的斜率分別是m1與m2
(1) 若L1//L2,則m1 = m2;反之亦然。
(2) 若L1 ^ L2,則m1 ´ m2 = - 1;反之亦然。
3. 直線方程式的求法:
(1) 點斜率
?經過點P(x0,y0)且斜率為m的直線方程式為y
-
y0 = m(x
-
x0)。
?經過點P(x0,y0)且斜率不存在的直線方程式為x
=
x0。
(2) 兩點式
經過相異兩點P(x1,y1)與Q(x2,y2)的直線方程式為
?當x1
¹
x2時,直線方程式為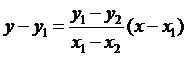 。
。
?當x1
=
x2時,直線方程式為x
=
x1。
(3) 斜截式
?斜率為m且y截距為b的直線方程式為y
=
mx +
b。
?斜率為m且x截距為a的直線方程式為y
=
m(x -
a)。
?斜率不存在且x截距為a的直線方程式為x
=
a。
(4) 截距式
x截距為a、y截距為b(a
¹
0,b
¹
0)的直線方程式為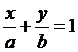 。
。
4. 由直線方程式求斜率:
設直線方程式ax
+
by +
c =
0,則
(1) 若b = 0,直線方程式的斜率不存在。
(2) 若b
¹
0,直線方程式的斜率為![]() 。
。
5. 如果直線L:ax + by + c = 0的斜率存在,則
(1) 和L平行的直線必可化簡為ax + by + k = 0(k ¹ c)。
(2) 和L垂直的直線必可化簡為bx - ay + h = 0。
6. 點與直線的距離:
點P(x1,y1)到直線L:ax
+
by +
c =
0的距離為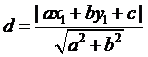 。
。
7. 兩平行線的距離:
兩平行線L1:ax
+
by +
c1 =
0與L2:ax
+
by +
c2 =
0的距離為 。
。
1. 函數f (x) = ax + b稱為線性函數,其圖形為一直線。
2. 二次函數f
(x) =
ax2 +
bx +
c圖形的對稱軸為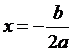 。
。
3. 若a
>
0,則f
(x) =
ax2 +
bx +
c在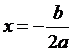 時f
(x)有最小值
時f
(x)有最小值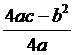 ,圖形頂點即最低點為
,圖形頂點即最低點為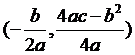 。
。
4. 若a
<
0,則f
(x) =
ax2 +
bx +
c在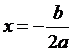 時f
(x)有最大值
時f
(x)有最大值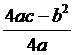 ,圖形頂點即最高點為
,圖形頂點即最高點為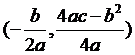 。
。
1. 有向角:
有方向限制的角稱為有向角。往逆時針方向旋轉的角稱為正角;往順時針方向旋轉的角稱為負角。
2. (1) 六十分制
將一圓周分成360等分,每一等分所對的圓心角即為1度。
(2) 弧度制
在圓周上取一與半徑等長之弧,此弧所對的圓心角即為1弧度。
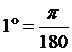 弧度 或 1弧度
弧度 或 1弧度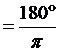
3. 已知一扇形之半徑為r,弧長為S,圓心角為q
弧度,面積為A,則
S =
rq,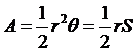 。
。
4. 同界角:
當兩個角有共同的始邊和終邊的時候,這兩個角稱為同界角。
5. 標準位置角:
將廣義角放在坐標平面上,角的頂點在原點上,角的始邊在x軸的正向上,這樣的有向角稱為標準位置角。
▲圖2-48

1.
銳角三角函數定義:
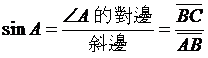 ,稱作ÐA的正弦函數
,稱作ÐA的正弦函數
 ,稱作ÐA的餘弦函數
,稱作ÐA的餘弦函數
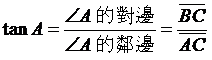 ,稱作ÐA的正切函數
,稱作ÐA的正切函數
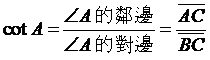 ,稱作ÐA的餘切函數
,稱作ÐA的餘切函數
 ,稱作ÐA的正割函數
,稱作ÐA的正割函數
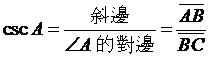 ,稱作ÐA的餘割函數
,稱作ÐA的餘割函數
2. 特別角三角函數值:
|
函數值 角度 |
sinq |
cosq |
tanq |
cotq |
secq |
cscq |
|
|
|
|
|
|
|
2 |
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
2 |
|
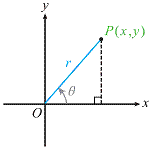
3. 任意角三角函數定義:
在標準位置角q
的終邊上任取一點P(x,y),假設![]()
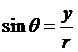 ,
,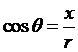 ,
,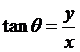
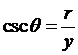 ,
, ,
,
4. 三角函數值的正負符號:
|
正負 函數 |
第一象限角 |
第二象限角 |
第三象限角 |
第四象限角 |
|
sinq、cscq |
+ |
+ |
- |
- |
|
cosq、secq |
+ |
- |
- |
+ |
|
tanq、cotq |
+ |
- |
+ |
- |
5. 象限角三角函數值:
|
函數值 角度 |
sinq |
cosq |
tanq |
cotq |
secq |
cscq |
|
0° |
0 |
1 |
0 |
無意義 |
1 |
無意義 |
|
|
1 |
0 |
無意義 |
0 |
無意義 |
1 |
|
180°(p ) |
0 |
- 1 |
0 |
無意義 |
- 1 |
無意義 |
|
|
- 1 |
0 |
無意義 |
0 |
無意義 |
- 1 |
6. 三角函數之間具有的關係:
(1) 倒數關係
sinq
cscq
=
1,cosq
secq
=
1,tanq
cotq
=
1
(2)
商數關係
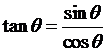 ,
,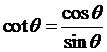
(3)
平方關係
sin2q
+
cos2q
=
1,1
+
tan2q
=
sec2q,1
+
cot2q
=
csc2q
1. y
= sinx的圖形可知
(1)y =
sinx的圖形的週期為2p
(2)
- 1
£
sinx £
1
2. y
= cosx的圖形可知
(1)y =
cosx的圖形的週期為2p
(2)
- 1
£
cosx £
1
3. y
= tanx的圖形可知
(1)y =
tanx的圖形的週期為p
(2)tanx的值可為任意實數
4. y
= cotx的圖形可知
(1)y =
cotx的圖形的週期為p
(2)cotx的值可為任意實數
5. y
= secx的圖形可知
(1)y =
secx的圖形的週期為2p
(2)secx
£
-
1或secx
³
1
6. y
= cscx的圖形可知
(1)y =
cscx的圖形的週期為2p
(2)cscx
£
-
1或cscx
³
1
在△ABC中,若a、b、c分別表ÐA、ÐB、ÐC的對邊長,以D表三角形面積,R為△ABC的外接圓半徑
(1) 面積公式
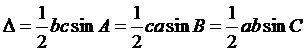
(2) 正弦定理
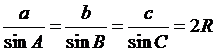
(3) 餘弦定理
a2 =
b2 + c2
-
2bccosA,b2
=
c2 + a2
-
2cacosB,c2
=
a2 +
b2 -
2abcosC
1. ![]() ,其中a1稱為
,其中a1稱為![]() 的x分量,a2稱為
的x分量,a2稱為![]() 的y分量。
的y分量。
![]() 的長度記作
的長度記作![]() 且
且![]() 。
。
2. 向量的坐標表示法:
設A(x1,y1)、B(x2,y2)為坐標平面上兩點,則![]() ,且
,且![]() 。
。
3. 相等向量:
設![]() ,
,![]() ,當a1
=
b1且a2
=
b2時,兩向量相等,記作
,當a1
=
b1且a2
=
b2時,兩向量相等,記作![]() 。反之,當
。反之,當![]() 時,a1
=
b1且a2
=
b2。
時,a1
=
b1且a2
=
b2。
4. 方向角:
對於非零向量![]() ,以x軸正向為始邊,
,以x軸正向為始邊,![]() 所在射線為終邊所夾的角度q(0
£
q
<
2p),稱為
所在射線為終邊所夾的角度q(0
£
q
<
2p),稱為![]() 的方向角即
的方向角即![]() 。
。
1. 向量加減與實數積的坐標表示法:
設![]() ,
,![]() ,r為實數,則
,r為實數,則
(1) ![]() 。
。
(2) ![]() 。
。
(3) ![]() 。
。
2. 向量的平行:
設![]() ,
,![]() ,則
,則![]() Û a1b2
=
a2b1;當b1b2
¹
0時,
Û a1b2
=
a2b1;當b1b2
¹
0時,
![]() Û
Û 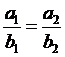 。
。
1. 向量內積的定義:
設![]() 與
與![]() 為兩非零向量,q
為兩向量的夾角,則
為兩非零向量,q
為兩向量的夾角,則![]() 與
與![]() 的內積
的內積![]() 。當
。當![]() 、
、![]() 有一向量為零向量時,規定
有一向量為零向量時,規定![]() 。
。
2. 向量內積的坐標表示法:
設![]() 與
與![]() ,則
,則![]() 。當
。當![]() 、
、![]() 有一向量為零向量時,
有一向量為零向量時,![]() 亦能成立。
亦能成立。
3. 向量的垂直(![]() 、
、![]() 為非零向量):
為非零向量):
![]() Û
Û ![]() 。
。
4. 向量內積的性質:設![]() 、
、![]() 與
與![]() 為坐標平面上三向量,r為實數,則
為坐標平面上三向量,r為實數,則
(1)![]() 。
(2)
。
(2)![]() 。
。
(3)![]() 。
(4)
。
(4)![]() 。
。
1. 正射影長:
設![]() 與
與![]() 為兩非零向量,q
為兩向量的夾角,則
為兩非零向量,q
為兩向量的夾角,則![]() 在
在![]() 的正射影長為
的正射影長為![]() 。
。
2. 點到直線距離:
在坐標平面上,已知點P(x1,y1)與直線L:ax
+
by +
c =
0,則P點到直線L的距離為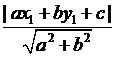 。
。
1. 多項式相等:
f (x) =
anxn
+ an
-
1xn
-
1
+
…
+ a1x
+
a0(an
¹
0)與g(x)
=
bmxm
+ bm
-
1xm
-
1
+
…
+ b1x
+
b0(bm
¹
0),當n
=
m且an
=
bn,an
-
1
= bn
-
1,…,a1
=
b1,a0
=
b0時,稱f
(x)與g(x)相等。
2. 多項式的定義:
設n為正整數或零且an、an
-
1、an
-
2、…、a1、a0都是實數,
f (x) =
anxn
+ an
-
1xn
-
1
+
…
+ a1x
+
a0,則稱f
(x)為x的多項式。
(1) 若an ¹ 0時,n稱為f (x)的次數,我們以degf (x) = n表示,或稱f (x)為n次多項式。
(2) ak稱為f (x)的xk項係數。
(3) 若an ¹ 0時,an稱為f (x)的領導係數。
(4) a0為f (x)的常數項。
3. 常數多項式:
若f
(x) =
a0時,f
(x)稱為常數多項式,又
(1) 當a0 ¹ 0時,f (x)稱為零次多項式,例如f (x) = 3。
(2) 當a0 = 0時,也就是f (x) = 0,f (x)稱為零多項式。
4. 除法定理:
設f
(x)與g(x)為二多項式,且g(x)
¹
0,則恰存在二多項式q(x)與r(x)滿足f
(x) =
g(x)q(x)
+ r(x),其中r(x)
=
0或degr(x)
<
degg(x),即被除式
=
除式
´
商式
+
餘式,其中餘式為0或餘式次數
<
除式次數。
1. 餘式定理:
設a
¹
0,多項式f
(x)除以ax
-
b的餘式為![]() 。
。
2. 因式定理:
設a
¹
0,若ax
-
b為多項式f
(x)的因式,則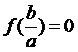 ,反之亦然。
,反之亦然。
3. 乘法公式:
(1) 和平方公式 (a
+
b)2 =
a2 +
2ab +
b2,
差平方公式 (a
-
b)2 =
a2 -
2ab +
b2。
(2) 平方差公式 a2 - b2 = (a + b)(a - b)。
(3) 立方和公式 (a
+
b)(a2
- ab
+
b2) =
a3 +
b3,
立方差公式 (a
-
b)(a2
+ ab
+
b2) =
a3 -
b3。
4. 一次因式檢驗法:
設f
(x) =
anxn
+ an
-
1xn
-
1
+
…
+ a1x
+
a0且an、an
-
1、an
-
2、…、a1、a0都是整數,若一次式ax
-
b為f
(x)的因式,其中a、b互質,則a為an的因數且b為a0的因數。
1. 一次方程式:
設a、b都是實數,則ax
+
b =
0稱為一次方程式:
(1) 若a
¹
0,則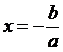 (恰有一解)。
(恰有一解)。
(2) 若a = 0,b ¹ 0,則ax + b = 0無解。
(3) 若a = 0,b = 0,則ax + b = 0的解為任意實數,也就是此方程式有無限多解。
2. 二次方程式解的判別:
設二次方程式ax2
+
bx +
c =
0:
(1) 當b2
-
4ac >
0時:ax2
+
bx +
c =
0有二相異實數解,且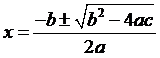 。
。
(2) 當b2
-
4ac =
0時:ax2
+
bx +
c =
0有二相等實數解,且 。
。
(3) 當b2 - 4ac < 0時:ax2 + bx + c = 0無實數解。
3. 根與係數關係:
設a、b
為二次方程式ax2
+
bx
+
c
=
0的兩根,則
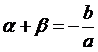 ,
,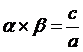 。
。
4. 由根假設方程式:
設a、b
為某二次方程式的兩根且此方程式的x2項係數為1,則此方程式為x2
-
(a
+
b
)x
+
(a
´
b
) =
0。
5. 一般而言,高次方程式anxn + an - 1xn - 1 + … + a1x + a0 = 0沒有固定的解法,可先嘗試利用公式或一次因式檢驗法將方程式因式分解,再求方程式的解。
1. 指數定義:
若a為實數且n為正整數,則 ,讀作「a的n次方」,其中a稱為底數,n為指數。
,讀作「a的n次方」,其中a稱為底數,n為指數。
2. 零指數與負整數指數:
若a為實數(但a
¹
0)且m、n為正整數,規定
(1)a0 =
1 (2) (3)
(3) 。
。
3. 方根的乘除運算:
若a
>
0,b
>
0且n為正整數,則
(1)![]() (2)
(2) 。
。
4. 分數指數:
若a
>
0且m為整數、n為正整數,規定:
(1)![]() (2)
(2)![]() 。
。
5. 實數指數律:
若r、s為實數且a
>
0、b
>
0,則
(1) ar ´ as = ar + s。
(2)  。
。
(3) (ar)s = ars。
(4) (ab)r = ar ´ br。
(5)  。
。
1. 指數函數定義:
設a
>
0且a
¹
1,對於任意實數x,y
=
ax稱為以a為底數的指數函數。
2. 指數函數y = ax的圖形:
(1) y = ax的圖形必在x軸上方,即指數函數值一定為正數。
(2) y = ax的圖形一定過點(0,1)。
(3) 當a
>
1時,y隨x增加而增加。
當0
< a
<
1時,y隨x增加而減少。
3. 指數相等:
設a
>
0且a
¹
1,x
>
0,y
>
0則ax
=
ay Û x
=
y。
1. 對數定義:
若a
>
0且a
¹
1,則ax
=
b Û x
=
logab。
2. 對數性質:
若a、M、N均為正實數且a
¹
1,則
(1) loga1 = 0,logaa = 1。
(2) ![]() 。
。
(3) loga(M ´ N) = logaM + logaN。
(4)  。
。
(5) logaM s = slogaM。
(6)  (r
¹
0)。
(r
¹
0)。
(7)  (換底公式,b
>
0且b
¹
1)。
(換底公式,b
>
0且b
¹
1)。
1. 對數函數定義:
設a
>
0且a
¹
1,x
>
0,y
=
logax稱為以a為底數的對數函數。
2. 對數函數y = logax的圖形:
(1) y = logax的圖形一定在y軸右方。
(2) y = logax的圖形一定過點(1,0)。
(3) 當a
>
1時,y隨x增加而增加。
當0
< a
<
1時,y隨x增加而減少。
3. 指數函數圖形與對數函數圖形的比較:
(1) y
= ax與 的圖形對稱於y軸。
的圖形對稱於y軸。
(2) y
= logax與![]() 的圖形對稱於x軸。
的圖形對稱於x軸。
(3) y = ax與y = logax的圖形對稱於直線y = x。
4. 對數相等:
設a
>
0且a
¹
1,x
>
0,y
>
0,則logax
=
logay Û x
=
y。
1. 對於每一個正數x,logx = n + logb(0 £ logb < 1,n為整數),整數n稱為對數logx的首數;logb稱為對數logx的尾數,尾數logb必為介於0與1之間的數。
2. 首數與尾數:
(1) 對數 = 首數 + 尾數(0 £ 尾數 < 1)。
(2) 真數x > 1,且整數的部分是n位數時,對數logx的首數是n - 1。
(3) 真數0 < x < 1,而其小數部分在小數點後第n位以前均為0,且第n位不是0,則數對logx的首數為 - n。
1. (1) 當a
>
0時,一次不等式ax
+
b >
0的解為 ,如圖1-26所示。
,如圖1-26所示。
(2) 當a
<
0時,一次不等式ax
+
b >
0的解為 ,如圖1-27所示。
,如圖1-27所示。

▲圖1-26 ▲圖1-27
2. 對於任一正數a,(1)|
x | £
a的解為
- a
£
x £
a,如圖1-28所示。
(2)| x |
³ a的解為x
£
-
a或x
³
a,如圖1-29所示。

▲圖1-28 ▲圖1-29
3. 二次函數y = ax2 + bx + c,
(1) 設a
>
0,則當b2
-
4ac >
0時,y
=
ax2 +
bx +
c的圖形為開口向上的拋物線且與x軸有兩個交點(a,0)與(b,0)其中 、
、 ,a
<
b,如圖1-30所示。
,a
<
b,如圖1-30所示。

▲圖1-30
所以不等式ax2
+
bx +
c <
0的解為a
<
x
<
b;
而不等式ax2
+
bx +
c >
0的解為x
<
a
或x
>
b。
(2)
設a
>
0,則當b2
-
4ac
=
0時,y
=
ax2
+
bx
+
c的圖形為開口向上的拋物線且與x軸有一個交點 ,如圖1-31所示。
,如圖1-31所示。

▲圖1-31
所以不等式ax2
+
bx +
c <
0無解;
不等式ax2
+
bx +
c £
0的解為 ;
;
不等式ax2
+
bx +
c >
0的解為x不等於![]() 的任意實數;
的任意實數;
不等式ax2
+
bx +
c ³
0的解為所有實數。
(3) 設a > 0,則當b2 - 4ac < 0時,y = ax2 + bx + c的圖形為開口向上的拋物線且與x軸沒有交點,如圖1-32所示。

▲圖1-32
所以不等式ax2
+
bx +
c <
0無解;
不等式ax2
+
bx +
c £
0無解;
不等式ax2
+
bx +
c >
0的解為所有實數;
不等式ax2
+
bx +
c ³
0的解為所有實數。
1. 二元一次不等式的圖形:設直線L:y = mx + b,則
(1) y > mx + b的圖形為直線L的上側半平面。
(2) y ³ mx + b的圖形為直線L及直線L的上側半平面。
(3) y < mx + b的圖形為直線L的下側半平面。
(4) y £ mx + b的圖形為直線L及直線L的下側半平面。
2. 設直線L:ax + by + c = 0,其中a > 0,則
(1) ax + by + c > 0的圖形為直線L的右側半平面。
(2) ax + by + c ³ 0的圖形為直線L及直線L的右側半平面。
(3) ax + by + c < 0的圖形為直線L的左側半平面。
(4) ax + by + c £ 0的圖形為直線L及直線L的左側半平面。
3. 二個或二個以上的二元一次不等式聯立時,是指同時滿足二個或二個以上的二元一次不等式,其圖形為各不等式圖形的共同部分。
1. 在數對(x,y)滿足一組二元一次聯立不等式的條件下,考慮二元一次函數f (x,y)的最大值、最小值:在此問題中,二元一次聯立不等式稱為問題的限制條件;滿足此條件的解,稱為問題的可行解,並稱可行解所圍區域為問題的可行解區域;又二元一次函數f (x,y)稱為此問題的目標函數,而使函數f (x,y)有最大值、最小值的數對(x,y),稱為問題的最佳解。
1. 圓的標準式:以O(h,k)為圓心,且半徑為r(r > 0)的圓方程式是(x - h)2 + (y - k)2 = r2。
2. 圓的一般式:圓方程式必為形式如x2 + y2 + dx + ey + f = 0的二元二次方程式,其中x2項與y2項的係數相等且方程式中不含xy項。
3. (1) 若d2
+
e2 -
4f >
0,則方程式x2
+
y2 +
dx +
ey +
f =
0表示一個圓,其圓心坐標為 ,半徑為
,半徑為 。
。
(2) 若d2
+
e2 -
4f =
0,則方程式x2
+
y2 +
dx +
ey +
f =
0表示一個點,此點坐標為 。
。
(3) 若d2 + e2 - 4f < 0,則方程式x2 + y2 + dx + ey + f = 0在坐標平面上沒有圖形。
4. 我們稱d2 + e2 - 4f為x2 + y2 + dx + ey + f = 0圖形的判別式。
1. 予點P之坐標為(x1,y1),圓C之方程式為(x - h)2 + (y - k)2 = r2。
(1) 若點P在圓C的內部,則(x1 - h)2 + (y1 - k)2 < r2,反之亦然。
(2) 若點P在圓C上,則(x1 - h)2 + (y1 - k)2 = r2,反之亦然。
(3) 若點P在圓C的外部,則(x1 - h)2 + (y1 - k)2 > r2,反之亦然。
2. 予點P之坐標為(x1,y1),圓C之方程式為x2 + y2 + dx + ey + f = 0。
(1) 若點P在圓C的內部,則x12 + y12 + dx1 + ey1 + f < 0,反之亦然。
(2) 若點P在圓C上,則x12 + y12 + dx1 + ey1 + f = 0,反之亦然。
(3) 若點P在圓C的外部,則x12 + y12 + dx1 + ey1 + f > 0,反之亦然。
3. 予直線L:ax
+
by +
c =
0與圓C:(x
-
h)2 +
(y -
k)2 =
r2,設圓心O與直線L的距離為d,則 。
。
(1) 若d < r,則直線L與圓C相割,反之亦然。
(2) 若d = r,則直線L與圓C相切,反之亦然。
(3) 若d > r,則直線L與圓C相離,反之亦然。
4. 切線方程式的求法:
(1) 過圓上一點,求切線方程式:
?
過圓C:(x
-
h)2 +
(y -
k)2 =
r2上一點P(x1,y1)的切線方程式為
(x1
- h)(x
- h)
+
(y1 -
k)(y -
k) =
r2。
?
過圓C:x2
+
y2 +
dx +
ey +
f =
0上一點P(x1,y1)的切線方程式為
 。
。
(2) 過圓外一點,求切線方程式:
予圓C:(x
-
h)2 +
(y -
k)2 =
r2與圓外一點P(x1,y1)。
則可依下列步驟求出過點P且與圓C相切的直線方程式:
?
找出圓心(h,k)與半徑r。
?
假設切線斜率為m,由點斜式可得切線方程式為y
-
y1 =
m(x -
x1),整理得
mx -
y -
mx1 +
y1 =
0。
?
利用圓心(h,k)到切線mx
-
y -
mx1 +
y1 =
0的距離等於圓C的半徑,
得 ,藉之以求m之值。
,藉之以求m之值。
?
將m值代入mx
-
y -
mx1 +
y1 =
0,即得過P點且與圓C相切的直線方程式。
5. 圓的切線段長之求法:
(1) 自點P(x1,y1)到圓C:(x
-
h)2 +
(y -
k)2 =
r2的切線段長為![]() 。
。
(2) 自點P(x1,y1)到圓C:x2
+
y2 +
dx +
ey +
f =
0的切線段長為![]() 。
。
1. 一個數列的項數有限,我們就稱這個數列為有限數列;若項數無限,則稱為無窮數列。
2. 已知 (å讀作sigma),c為常數,則
(å讀作sigma),c為常數,則
(1)  。
。
(2)  。
。
(3)  。
。
(4)  ,其中1
£
m <
n且m為整數。
,其中1
£
m <
n且m為整數。
3. 若在一個數列中,除了首項外,其任意一項與前一項的差都相等,我們就稱此數列為等差數列(或算術數列);其固定的差稱為公差。
4. 設一等差數列的首項為a1,公差為d,一般項為an,前n項的和為Sn,
則an
=
a1 +
(n -
1)d
 。
。
5. 設a、b、c三個數成等差數列,則等差中項 。
。
1. 予一數列,其中每一項皆不為0。若此數列除首項之外,其任意一項與前一項的比值都相等,我們就稱此數列為等比數列(或幾何數列);此固定的比值稱為此數列之公比。
2. 設a、b、c三個數成等比數列,則等比中項![]() 。
。
3. 已知一個等比數列的首項為a1,公比為r,則
(1) 此等比數列的一般項為an = a1 ´ rn - 1。
(2) 當r = 1時,前n項的和Sn = na1。
(3) 當r
¹
1時,前n項的和 。
。
1. 計數時,可以將一些原本零散沒有組織的東西,將它組織成像樹枝分叉一層一層拓展開來的結構形式,這樣的圖形稱為樹狀圖。
2. 加法原理:
如果完成某件事,有k個不同的方式,採用方式一有m1種方法,採用方式二有m2種方法,……,採用方式k有mk種方法,則完成這件事的方法共有m1
+
m2 +
…
+ mk種。
3. 乘法原理:
如果完成某件事須經過k個步驟,而完成第一個步驟有m1種方法,完成第二個步驟有m2種方法,……,完成第k個步驟有mk種方法,每個步驟間所選用的方法互不影響,則完成這件事的方法共有m1
´
m2 ´
…
´ mk種。
1. 相異物的直線排列:
(1) 由n個不同的事物中,全取排成一列的排列方法數為
![]() 。
。
(2) 從n個不同的事物中,任選m個排成一列的排列方法數為
 。
。
2. 不盡相異物的直線排列:
(1) 設n個事物中有m個相同,其餘都不同。則n件全取的排列方法數為![]() 。
。
(2) 設n個事物中,可分成k組。其中第一組有m1個相同物,第二組有m2個相同物,……,第k組有mk個相同物(此時m1
+
m2 +
…
+ mk
=
n),則此n個事物全取排成一列,其排列方法數為 。
。
3. 環狀排列:
(1) 將n個不同的事物作環狀排列,其排列方法數為 。
。
(2) 從n個不同的事物中,任選m個作環狀排列,其排列方法數為
 。
。
4. 組合:
從n件不同的事物中,每次不重複的取m個為一組,其組合數為
 。
。
(1) ![]() (0
£
m £
n)。
(0
£
m £
n)。
(2) ![]() 。
。
1. 集合是由一些明確的事物所組成,組成這個群體的每個事物稱為這個集合的元素。
2. 空集合:
不包含任何元素的集合稱為空集合,以符號{ }或Æ來表示。
3. 子集:
如果集合B中的每一個元素都是集合A的元素,稱集合B為集合A的子集。
4. 聯集:
集合A所有的元素與集合B所有的元素所組成的集合,稱為A與B的聯集,記為AÈB,即AÈB
=
{x | xÎA或xÎB}。
5. 交集:
集合A與集合B的共同元素所組成的集合,稱為A與B的交集,記為AÇB,即AÇB
=
{x | xÎA且xÎB}。
6. 差集:
由屬於集合A,但不屬於集合B的元素所組成的集合,稱為A與B的差集,記為A
-
B,即A
-
B =
{x | xÎA但xÏB}。
7. 宇集與補集:
當所探討的集合都是某個集合U的子集時,稱U為宇集。當A是宇集U的子集時,稱U中不屬於A的元素組成的集合為A在U中的補集。
8. 一項隨機試驗中,所有可能發生的結果所形成的集合,叫做試驗的樣本空間,通常用S表示。樣本空間中的每一個元素,稱為一個樣本。樣本空間的每個子集稱為一個事件。
9. 設A、B為樣本空間S中的兩個事件,
(1) 和事件:AÈB表示事件A與事件B所有的樣本所構成的事件,稱為和事件。
(2) 積事件:AÇB表示事件A與事件B共有的樣本所構成的事件,稱為積事件。
(3) 餘事件:A¢表示不在A中的樣本所構成的事件,稱為餘事件。
(4) 互斥事件:如果AÇB = Æ,則稱A、B兩個事件互斥,也就是事件A與事件B不可能同時發生。
1. 假設一個隨機試驗的樣本空間S,為有有限個樣本,其中各樣本點出現的機會均等。若AÌS為一事件,則事件A發生的機率為A之元素個數與S之元素個數的比值,記為 ,其中n(S)與n(A)分別表示S與A的元素個數。
,其中n(S)與n(A)分別表示S與A的元素個數。
2. 機率的性質:
(1) P(Æ) = 0。
(2) P(S) = 1。
(3) 若AÌS為一事件,則0 £ P(A) £ 1。
(4) 餘事件的機率:若AÌS為一事件,則P(A¢) = 1 - P(A)。
(5) 若A和B為S中的兩事件且AÌB,則P(A) £ P(B)。
(6) 機率的排容原理:若A和B為S中的兩事件,則
P(AÈB)
=
P(A) +
P(B) -
P(AÇB)。
1. 設某事件發生的機率為P,若該事件發生時可得到的報酬為M,失敗時報酬為0,則M ´ P稱為此事件的數學期望值,簡稱為期望值,通常以E表示。
2. 設一試驗的樣本空間S可分割成k個互斥事件,而每個事件發生機率分別為P1、P2、……、Pk,且事件發生時分別可得數值M1、M2、……、Mk的報酬,則M1 ´ P1 + M2 ´ P2 + … + Mk ´ Pk稱為此試驗的數學期望值,簡稱為期望值。
1. 製作次數分配表的步驟:
排序、求全距、定組數或組距、定組限、歸類並計算次數。
2. 直方圖:
利用長方形來表示數值資料中,各組的次數分布的情況,稱為直方圖。
3. 次數分配折線圖:
以各組資料的組中點為橫坐標,以各組的次數為縱坐標標示出各點,由左而右連接相鄰的點,並於最左邊與最右邊各向外延伸一點,就形成一折線圖。
4. 累積次數分配曲線圖:
利用累積次數分配表,以各組資料的上限為橫坐標,及各組累積的次數為縱坐標標示出各點,由左而右連接相鄰的點,即得以下累積分配曲線圖;以各組資料的下限為橫坐標,及各組累積的次數為縱坐標標示出各點,由左而右連接相鄰的點,即得以上累積分配曲線圖。
1. 算術平均數:
設一群數值為x1、x2、……、xn,則其算術平均數![]() 定義為
定義為
 。
。
2. 中位數:
設n個數值由小至大排列為x(1)
£
x(2) £
…
£ x(n),
(1) 若n為奇數時,中位數![]() 。
。
(2) 若n為偶數時,中位數 ,即正中間兩個數的平均。
,即正中間兩個數的平均。
3. 眾數:
一群數值中出現次數最多的數稱為眾數,記作Mo。又眾數可能不只一個。
4. 百分等級:
當某個資料數值,在整體資料中有至少k%的資料數值小於或等於它,而且有至少(100
-
k)%的資料數值大於或等於它,我們稱這個資料數值的百分等級為k,記作PR
=
k。
1. 全距是指一群數值資料中,最大值和最小值的差距,通常以R表示。
2. 四分位距:
設n個數值由小至大排列為x(1)
£
x(2) £
…
£ x(n),將已排列的數值等分成四段,可得三個分界點,最小的分界點稱為第1四分位數,以Q1表示;其次即為中位數;最後的分界點稱為第3四分位數,以Q3表示。第3四分位數Q3與第1四分位數Q1的差稱為四分位距,以IQR表示,即IQR
=
Q3 -
Q1。
3. 設n個數值x1、x2、……、xn;以![]() 表示其算術平均數,我們稱
表示其算術平均數,我們稱![]() 為xi的離均差。離均差平方的算術平均數稱為變異數,而變異數的正平方根稱為標準差。設n個資料為x1、x2、……、xn,其算術平均數為
為xi的離均差。離均差平方的算術平均數稱為變異數,而變異數的正平方根稱為標準差。設n個資料為x1、x2、……、xn,其算術平均數為![]() ,則標準差為
,則標準差為 。
。
1. 簡單隨機抽樣:
從母群體中,每一個體被選中的機會都相等的條件下,隨機抽取樣本,稱為簡單隨機抽樣。
2. 系統抽樣:
系統抽樣為做一次簡單隨機抽樣後,依據固定間隔數抽出下一個樣本。
3. 分層隨機抽樣:
將母群體依某種標準區分成不重複的若干組,每組稱為「層」,且層與層之間有很大的變異性,同一層內的變異性較小。再從每一層中利用簡單隨機抽樣抽出所需比例的樣本數,將所得各層樣本合起來即為樣本。
4. 部落抽樣:
其方法為將母群體分成若干部落,而部落間的變異小,部落內的變異大。再從這些部落中抽出數個部落進行抽樣調查或普查。
1. 媒體報導中的滿意度是抽樣受訪民眾的滿意度,將它加上正負抽樣誤差,就得一個信賴區間,而我們有95%的信心說,真正滿意的比例會落在信賴區間內。
1. 數線:數線上相異兩點A(x1)、B(x2),則
(1) ![]()
(2) ![]() 的中點為
的中點為
2. 坐標平面:將平面分為四象限

▲圖1-36
1. 坐標平面上相異兩點A(x1,y1)、B(x2,y2),則
(1) 距離公式:![]()
(2) 中點公式:![]() 的中點為
的中點為
(3) 若A
-
P -
B,且![]() ,則
,則
內分點公式:
2. 設A(x1,y1)、B(x2,y2)、C(x3,y3)為△ABC的三頂點,則
△ABC的重心為
1. 函數的定義:
設x、y是兩個變數,如果給定x值後、y值隨著x值依某種關係而確定,我們稱y為x的函數,x稱為自變數,y稱為應變數。
2. 函數圖形:
(1) 常數函數(線型函數),形如y = k
(2) 一次函數(線型函數),形如y = ax + b
(3) 二次函數(拋物線),形如y = ax2 + bx + c
1. 直線的斜率: (x1
¹
x2)
(x1
¹
x2)
2. 判別斜率大小:

▲圖1-37
3. 平行與垂直:
平面上相異兩直線L1、L2的斜率分別為m1、m2(m1
¹
0,m2
¹
0),則
(1) L1//L2 Û m1 = m2
(2) L1 ^ L2 Û m1 ´ m2 = - 1
4. 直線方程式:
(1) 點斜式:直線L過P(x0,y0)且斜率為m,則L:y - y0 = m(x - x0)
(2) 兩點式:直線L過P1(x1,y1)、P2(x2,y2)兩點且x1
¹
x2
則L:
(3) 斜截式:直線L的斜率為m,若y截距為b
則L:y
=
mx +
b
(4) 截距式:直線L的x截距為a,y截距為b(ab
¹
0)
則L:
(5) 一般式:直線L為ax
+
by +
c =
0(a、b不同時為0),

(6) 平行線與垂直線:直線L:ax
+
by =
c,則
5. 二元一次方程組的解之幾何意義
兩直線的關係:方程組 ,(a1b1c1
¹
0,a2b2c2
¹
0)
,(a1b1c1
¹
0,a2b2c2
¹
0)
|
相容方程組 |
|
相交於一點 |
恰有一組解 |
|
|
矛盾方程組 |
|
平行 |
無解 |
|
|
相依方程組 |
|
重合 |
無限多組解 |
|
1. 角度互換:
(1)  (弧度)
(弧度)
(2) 1(弧度)
2. 同界角:
兩有向角a、b
有相同的始邊和終邊,即a
-
b
=
360°k(或2kp),其中k為整數,則a、b
互為同界角。
3. 扇形:
(1) 弧長S = rq
(2) 周長L = S + 2r
(3)
面積
1. 銳角三角函數的定義:
![]()
![]()
![]()

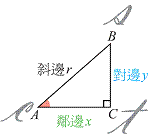
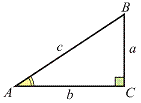
▲圖2-38







2. 三角函數的基本性質:
(1) 倒數關係:
sinq
cscq
=
1
cosq
secq
=
1
tanq
cotq
=
1
(2)
平方關係:
sin2q
+
cos2q
=
1
1
+
tan2q
=
sec2q
1
+
cot2q
=
csc2q
(3)
商數關係:


(4)
餘角關係:
sinq
=
cos(90°
-
q
)
tanq
=
cot(90°
-
q
)
secq
=
csc(90°
-
q
)
3. 特別角的三角函數:列出sin,cos,tan,其餘利用倒數可得。
|
函數 q |
sin |
cos |
tan |
|
30° |
|
|
|
|
45° |
|
|
1 |
|
60° |
|
|
|
▲圖2-39

1.
q
為標準位置角,且q
不是象限角
在其終邊上取一點P(x,y),![]() ,則
,則
 ,
, ,
,
 ,
, ,
,
2. 象限角的三角函數值:
|
函數 q |
sin |
cos |
tan |
|
0° |
0 |
1 |
0 |
|
90° |
1 |
0 |
|
|
180° |
0 |
- 1 |
0 |
|
270° |
- 1 |
0 |
|
3.
化任意角的三角函數值為銳角的三角函數值:
利用90°
± q,180°
± q,270°
± q,360°
± q(或
± q)和第一、第二、第三、第四象限角的三角函數值的正負作換算。

▲圖2-40
1. 三角函數的圖形:
|
三角函數圖形 |
週期 |
值域 |
|
▲圖2-41 |
2p |
- 1 £ y £ 1 (即| y | £ 1) |
|
▲圖2-42 |
2p |
- 1 £ y £ 1 (即| y | £ 1) |
|
▲圖2-43 |
p |
y為任意實數 |
|
▲圖2-44 |
p |
y為任意實數 |
|
▲圖2-45 |
2p |
y ³ 1或y £ - 1 (即| y | ³ 1) |
|
▲圖2-46 |
2p |
y ³ 1或y £ - 1 (即| y | ³ 1) |
2. 圖形變化:
|
f (x)
=
a |
|
1. 和差角公式:
sin(a
±
b
)
= sina
cosb
± cosa
sinb
cos(a
± b
) =
cosa
cosb![]() sina
sinb
sina
sinb
 (tana
tanb
¹
± 1)
(tana
tanb
¹
± 1)
2. 二倍角公式:
sin2q
=
2sinq
cosq
cos2q
=
cos2q
-
sin2q
=
2cos2q
-
1 =
1 -
2sin2q
 (tan2q
¹
1)
(tan2q
¹
1)
1. △ABC面積 (已知SAS)
(已知SAS)
![]() (海龍公式,已知SSS)
(海龍公式,已知SSS)
 (R:外接圓半徑)
(R:外接圓半徑)
=
rs(r:內切圓半徑)
2. 正弦定理:
(a:b:c
=
sinA:sinB:sinC)
3. 餘弦定理:
|
已知SAS |
已知SSS |
|
a2 = b2 + c2 - 2bccosA |
|
|
b2 = c2 + a2 - 2cacosB |
|
|
c2 = a2 + b2 - 2abcosC |
|
1. 解三角形:已知SSS、SAS由餘弦定理先解,其餘視情況而定。
2. 三角測量:畫圖(看三角形),利用三角函數或正餘弦定理解之。
1. (1) 有向線段:由起點A到終點B的線段,以![]() 表示
表示
(2) 向量:有大小有方向的量,但不考慮起點位置
2. 向量的坐標表示法:
A(x1,y1)、B(x2,y2),則
(1) ![]()
(2) ![]()
3. 特殊向量:
(1) 零
向
量:起點和終點重合的有向線段決定的向量,以
![]() 表示
表示
(2) 相等向量:兩向量大小相等方向相同
若![]() ,
,![]() ,且
,且![]()
則a1
=
b1,a2
=
b2
(3) 反
向
量:兩向量大小相等但方向相反
若![]() ,則
,則![]()
1. 加法圖示:
![]() (1)
三角形法:
(1)
三角形法:![]()
(2) 平行四邊形法
2. 單位向量:長度為1的向量,與![]() 同方向的單位向量為
同方向的單位向量為![]()
3. 坐標表示法:
![]() ,
,![]() ,r為實數,則
,r為實數,則
(1) ![]()
(2) ![]()
1. 內積:
![]() ,
,![]() ,且
,且![]() 、
、![]() 皆為非零向量,夾角為q
皆為非零向量,夾角為q
Þ ![]()
當![]() 或
或![]() 時,規定
時,規定![]() ,此時
,此時![]() 亦成立。
亦成立。
2. 垂直與平行:
![]() ,
,![]() ,且
,且![]() 、
、![]() 皆為非零向量,r為實數,則
皆為非零向量,r為實數,則
(1) ![]() Û
Û ![]() Û
Û  (b1b2
¹
0)
(b1b2
¹
0)
(2) ![]() Û
Û ![]() Û a1b1
+
a2b2
= 0
Û a1b1
+
a2b2
= 0
3. 內積的性質:
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
(5) ![]()
(6) ![]()
(7) ![]()
1. 正射影:設![]() 為非零向量,
為非零向量,
(1) ![]() 在
在![]() 上的正射影量
上的正射影量
(2) ![]() 在
在![]() 上的正射影長
上的正射影長
(3) ![]() 在
在![]() 上的正射影
上的正射影
2. (1) 點P(x0,y0)到直線L:ax
+
by +
c =
0的距離:

(2) 兩平行線 的距離:
的距離:

3. 向量方法求三角形面積:
設![]() ,
,![]() ,則由
,則由![]() 與
與![]() 為兩鄰邊所夾的
為兩鄰邊所夾的
三角形面積

1. 多項式:f
(x) =
anxn
+ an
-
1xn
-
1
+
……
+ a1x
+
a0(an
¹
0),
其中 。
。
(1) ak為xk的係數,a0稱為常數項
(2) an ¹ 0,an為領導係數,次數以degf (x) = n表示
(3) 常數多項式
2. 多項式的四則運算:
(1) 加減:同次項合併
(2) 乘除:分離係數
3. 綜合除法:右擺除式,前係數下拉,一乘一加得商式及餘式。而長除法是上下減。
1. 餘式定理:多項式f (x)除以x - a的餘式為f (a)。
2. 因式定理:x - a為多項式f (x)的因式 Û f (a) = 0。
1. 一元二次方程式:因式分解或公式解解之。
(1) 公式解ax2
+
bx +
c =
0 Þ 
(2) 根的性質:
|
判別式 |
根的性質 |
|
b2 - 4ac > 0 |
兩相異實根 |
|
b2 - 4ac = 0 |
兩相等實根 |
|
b2 - 4ac < 0 |
無實根(無實數解) |
(3) 根與係數:ax2
+
bx +
c =
0的兩根為a、b Þ 
1. 分式的四則運算:
(1) 加減:通分合併
(2) 乘除:約去公因式,化為最簡分式
2. 部份分式法:將最簡真分式化為若干個最簡真分式之和。
3. 分式方程式:同乘以分母最低公倍式得n次方程式求解,其解代回原式檢驗分母是否為零,若分母為零,則此根不合。
4. 根式的四則運算:
(1) 加減:同類根式合併
(2) 乘除:根式內的數直接乘除
※5.
二重根式:![]() (a
³
b ³
0)。
(a
³
b ³
0)。
1. 解一次方程組:
(1) 代入消去法
(2) 加減消去法
1. 二階行列式值的定義:
![]()

2. 三階行列式值的定義:
(1) 
(2) 行列式依某行或某列,及 降階(去同行同列)展開。
降階(去同行同列)展開。
3. 二階、三階行列式的性質:
(1) 行與列互換,其值不變。
(2) 任兩行或任兩列互相對調,其值差一負號。
(3) 任一行或任一列可提出公因數。
(4)
?任兩行或任兩列成比例時,其值為0。
?某行或某列的各元素為0,其值為0。
(5) 將某行(列)的k倍加到另一行(列),其值不變。
(6) 加法原則:依某行或某列可拆為兩行列式之和。
4. 克拉瑪公式:
(1) 二元一次方程組
令 ,
, ,
,

(2) 三元一次方程組
令
 ﹐
﹐ ,
,

1. 複數:
(1) z = a + bi(a、b為實數),其中a為實部,b為虛部
(2) 若a + bi = c + di,則a = c,b = d
(3) 若z
=
a +
bi,則共軛複數![]()
2. 複數的四則運算:
若z1
=
a +
bi,z2
=
c +
di
則(1)z1
± z2 =
(a ± c) +
(b ± d)i
(2)z1
´
z2 =
(ac -
bd) +
(ad +
bc)i
(3) (z2
¹
0)
(z2
¹
0)
3. 共軛複數的性質:
(1) ![]()
(2) ![]() ;
; (z2
¹
0)
(z2
¹
0)
(3) ![]()
4. 虛數單位![]() ,其特性為
,其特性為
(1) i4k = 1,i4k + 1 = i,i4k + 2 = - 1,i4k + 3 = - i(k為正整數)
(2) 1 + i + i2 + i3 = 0
(3) (1 ± i)2 = ± 2i
1. 方程式ax2
+
bx +
c =
0(a、b、c為實數),其解為
則
2. 方程式ax2 + bx + c = 0(a、b、c為實數),已知有一根p + qi,則必有另一根p - qi。
1. 複數的絕對值:
(1) 定義:若z
=
x +
yi(x、y為實數),![]()
(2) 性質:
?![]()
?![]()
?![]()
?![]()
? (z
¹
0)
(z
¹
0)
? (z2
¹
0)
(z2
¹
0)
2. 在直角坐標系中,設點P異於原點,直角坐標P(x,y),可以序對(r,q )表示之,此序對(r,q )稱為P點的極坐標,其中r為P點到原點的距離,稱為向徑,q 為以x軸正向為始邊旋轉到P點的有向角,稱為輻角。
(1) 直角坐標(x,y)異於原點轉換成極坐標(r,q
)
 (可直接畫圖求q)
(可直接畫圖求q)
(2) 極坐標(r,q
)轉換成直角坐標(x,y)

3. 複數的極式:
z =
x +
yi =
| z |(cosq
+
isinq
)
若0°
£
q
<
360°,則稱q
為z的主輻角,表為Arg(z)
=
q
1. 複數極式的乘除:
若z1
=
r1(cosq1
+
isinq2),z2
=
r2(cosq1
+
isinq2),則:
(1) z1 ´ z2 = r1r2[cos(q1 + q2) + isin(q1 + q2)]
(2)  (z2
¹
0)
(z2
¹
0)
2. 棣美弗定理:
複數z
=
r(cosq
+
isinq
),r
=
| z |,則:
zn =
rn(cosnq
+
isinnq
),n為整數(z
¹
0)
3. 複數的n次方根:
若xn
=
z =
| z |(cosq
+
isinq
),z
¹
0,n為自然數
則z的n次方根為
其中k
=
0,1,2,……,n
-
1,q
=
Arg(z)
1. 二元一次不等式:

2. 二元一次聯立不等式:
兩個或兩個以上的二元一次聯立不等式的圖形,是每一個不等式圖形的共同部分。
1. 線性規劃:
在滿足限制條件下,列出二元一次聯立不等式,藉以決定如何將有限的資源作最有效的調配與應用,能以最低的代價,獲得最高的效益,此過程稱為線性規劃。此聯立不等式的解稱為可行解,此聯立不等式的圖解區域稱為可行解區域,使能獲得最高利潤的一次函數f
(x,y)稱為目標函數。在可行解區域中能使目標函數為最大或最小的解,稱為最佳解。
2. 線性規劃應用問題的求解過程:
(1) 依題意列表整理。
(2) 依題意列不等式。
(3) 畫圖找出可行解區域的頂點。
(4) 頂點代入目標函數求極值。
一元二次不等式:
將不等式移項化簡得ax2 + bx + c > 0,ax2 + bx + c ³ 0,ax2 + bx + c < 0或ax2 + bx + c £ 0(a ¹ 0且a、b、c為實數)。
【結論一】
若a > 0,一元二次方程式ax2 + bx + c = 0的判別式D = b2 - 4ac > 0
(y = ax2 + bx + c的圖形與x軸相交兩點)
ax2 + bx + c = 0的兩根為a、b,且a < b
|
不等式 |
不等式的解 |
|
ax2 + bx + c > 0 |
x < a 或x > b |
|
ax2 + bx + c ³ 0 |
x £ a 或x ³ b |
|
ax2 + bx + c < 0 |
a < x < b |
|
ax2 + bx + c £ 0 |
a £ x £ b |
【結論二】
若a > 0,一元二次方程式ax2 + bx + c = 0的判別式D = b2 - 4ac = 0
(y = ax2 + bx + c的圖形與x軸相交一點)
|
不等式 |
不等式的解 |
|
ax2 + bx + c > 0可化為(x - h)2 > 0 |
x為任意實數但x ¹ h |
|
ax2 + bx + c ³ 0可化為(x - h)2 ³ 0 |
x為任意實數 |
|
ax2 + bx + c < 0可化為(x - h)2 < 0 |
x無實數解 |
|
ax2 + bx + c £ 0可化為(x - h)2 £ 0 |
x = h |
【結論三】
若a > 0,一元二次方程式ax2 + bx + c = 0的判別式D = b2 - 4ac < 0
(y = ax2 + bx + c的圖形與x軸無交點)
|
|
不等式 |
不等式的解 |
|
a > 0 |
ax2 + bx + c > 0 或ax2 + bx + c ³ 0 |
x為任意實數 |
|
ax2 + bx + c £ 0 或ax2 + bx + c < 0 |
x無實數解 |
1. 算幾不等式:
設a、b為兩正實數,則 (或寫成
(或寫成![]() )
)
其中
不等式的等號成立於a
=
b
2. 柯西不等式:
設兩非零向量![]() ,
,![]()
其中a1、a2、b1、b2為實數,則(a12
+ a22)(b12
+
b22)
³ (a1b1
+ a2b2)2
設b1b2
¹
0,柯西不等式的等號成立於![]()
即 ,若有一向量為零時,顯然等號成立。
,若有一向量為零時,顯然等號成立。
1. 數列與級數:
(1) 數列:將一系列的數依照順序排列出來,例如:a1,a2,a3﹐……﹐an,稱為數列。其中a1稱為首項或第1項,a2稱為第2項,……,an稱為第n項或末項。
(2) 級數:將數列áakñ的各項以「+」連接起來的式子,例如:
a1
+
a2 + a3
+
……
+ an,稱為級數,其表示法為![]() 。
。
(3) 有限項數「å」的運算性質:
? (c為常數)
(c為常數)
? (c為常數)
(c為常數)
?
? (1
£
m <
n)
(1
£
m <
n)
2. 等差數列:
在數列áakñ中,若後一項減去前一項的差都相等,我們稱這數列為等差數列(或算術數列),這個相等的差稱為此數列的公差,通常以d表示。
若首項為a1,公差為d,則第n項為
an
=
a1 +
(n -
1)d (末項
=
首項
+
間隔數
´
公差)
將等差數列中的am當成最前項,公差為d,則第n項為
an
=
am +
(n -
m)d (末項
=
某項
+
間隔數
´
公差)
3. 等差中項:
若a,b,c成等差數列,我們稱b為a與c的等差中項(或算術平均數),則 。
。
4. 等差級數:
若a1,a2,a3,……,an是一等差數列,將其前n項相加得a1
+
a2 + a3
+
……
+ an,就稱為等差級數(或算術級數),此級數前n項的和為
 。
。
(1) 已知等差級數首項a1,公差d,項數n,則 。
。
(2) 已知等差級數首項a1,末項an,項數n,則 。
。
1. 等比數列:
在數列áakñ中,若任一項與其前一項的比值都相等,我們稱這數列為等比數列,這個相等的比值稱為此數列的公比,通常以r表示。
若首項為a1,公比為r,則第n項為
an
=
a1rn
- 1 (末項
=
首項
´
公比間隔數)
將等比數列中的am當成最前項,公比為r,則第n項為
an
=
amrn
- m (末項
=
某項
´
公比間隔數)
2. 等比中項:
若a,b,c成等比數列,我們稱b為a與c的等比中項,則b2
=
ac,即![]() 。
。
3. 等比級數:
若a1,a2,a3﹐……﹐an是一等比數列,將其前n項相加得a1
+
a2 + a3
+
……
+ an,就稱為等比級數,此級數前n項的和為 。
。
已知等比級數首項a1,公比r,項數n,則
(1) 當r
¹
1時, 。
。
(2) 當r
=
1時, 。
。
1. 指數律:
對於每一個實數a,我們以記號an代表a自乘n次的乘積,其n為正整數,即 ,讀做「a的n次方」,其中a稱為底數,n稱為指數。
,讀做「a的n次方」,其中a稱為底數,n稱為指數。
2. 指數運算的性質:
若a、b為正實數,m、n為任意實數,則
(1) am ´ an = am + n;am ¸ an = am - n
(2) (am)n = am ´ n
(3) (a ´ b)n = an ´ bn
(4) a0 = 1(此時a ¹ 0)
(5)  (此時a
¹
0)
(此時a
¹
0)
(6) ![]() ;
;![]() (此時n為正整數)
(此時n為正整數)
1. 指數函數y = ax(a > 0且a ¹ 1)的圖形:
(1) y = ax的圖形皆在x軸上方,過點(0,1),且漸近線均為x軸。
(2) 當a > 1時,y = ax為遞增函數;當0 < a < 1時,y = ax為遞減函數。
(3) y
= ax與 的圖形對稱於y軸。
的圖形對稱於y軸。
2. 指數的比大小:
關於![]() 與
與![]() 的大小關係,分a
>
1和0
< a
< 1兩種情形比較:
的大小關係,分a
>
1和0
< a
< 1兩種情形比較:
|
a > 1 |
y = ax為遞增函數 |
若x1
>
x2,則 |
|
0 < a < 1 |
y = ax為遞減函數 |
若x1
>
x2,則 |
3. 指數方程式:
(1) 化為同底數,利用指數相等。
(2) 將ax看成未知數再解方程式(須滿足ax > 0)。
1. 對數的意義:
若a
>
0,a
¹
1,b
>
0,當ax
=
b時,我們用符號logab來表示x,即
ax =
b Û logab
=
x
我們稱logab為「以a為底數時b的對數」,其中b稱為真數。
2. 對數的性質:
設a、b、x、y均為正實數,且a
¹
1,b
¹
1
(1) loga1 = 0;logaa = 1
(2) loga(x
´ y)
=
logax +
logay;
(3) logaxn
= nlogax; (此時m、n為實數且m
¹
0)
(此時m、n為實數且m
¹
0)
(4)  (換底公式)
(換底公式)
(5) ![]()
1. 對數函數y = logax(a > 0,a ¹ 1且x > 0)的圖形:
(1) y = logax的圖形皆在y軸右方,過點(1,0),且漸近線均為y軸。
(2) 當a > 1時,y = logax為遞增函數;當0 < a < 1時,y = logax為遞減函數。
(3) y
= logax與![]() 的圖形對稱於x軸。
的圖形對稱於x軸。
(4) 對數函數y = logax(a > 0,a ¹ 1且x > 0)與指數函數y = ax(a > 0)的圖形對稱於直線y = x。
2. 對數的比大小:
關於logax1與logax2的大小關係,分a
>
1和0
< a
< 1兩種情形比較:
|
a > 1 |
y = logax為遞增函數 |
若x1 > x2,則logax1 > logax2,即真數愈大其值愈大,反之亦成立 |
|
0 < a < 1 |
y = logax為遞減函數 |
若x1 > x2,則logax1 < logax2,即真數愈大其值愈小,反之亦成立 |
3. 對數方程式:
(1) 化為同底數,利用真數相等。
(2) 將logax看成未知數再解方程式(須滿足真數x > 0)。
1. 常用對數:
logx =
n +
a,其中n為整數,且0
£
a
<
1,我們稱n為logx的首數,a
為logx的尾數。
2. 常用對數的首數與真數的位數:設n為非負整數,
(1) 真數x ³ 1且logx的首數為n,則x的整數部分為n + 1位數。
(2) 真數0 < x < 1且logx的首數為 - n,則x自小數點後第n位開始出現非零數字。
1. 加法原理:
若完成某件工作的方法可區分成k類,且第1類有m1種方法,第2類有m2種方法,……,第k類有mk種方法,則完成這件工作的方法共有m1
+
m2
+
……
+ mk種。
2. 乘法原理:
若完成某件工作的方法須經過k個步驟,且第1步驟中有m1種方法,第2步驟中有m2種方法,……,第k步驟中有mk種方法,則完成這件工作的方法共有m1
´
m2
´
……
´ mk種。
1. 完全相異物的直線排列:
(1) 將n個不同的事物排成一列的排列總數為
![]()
(2) 從n個不同的事物中任選m個(m £ n)排成一列的排列總數為

2. 有相同物的直線排列:
(1) 設n個事物有p個相同排成一列的總數為
![]()
(2) 設有n個事物,共有k種不同種類(同類中的事物相同),第1類有p1個,第2類有p2個,……,第k類有pk個(即n = p1 + p2 + …… + pk),將此n個事物排成一列的總數為

1. 相異物的組合:
從n個不同的事物中,取m個(m
£
n)為一組,其組合數為

1. 二項式定理:
對於任意正整數n,

其中![]() 稱為此展開式的一般項,
稱為此展開式的一般項,![]() 恰為展開式中第r
+
1項的係數。
恰為展開式中第r
+
1項的係數。
2. 性質:
(1) ![]()
(2) ![]()
1. 樣本空間:
一項試驗中所有可能發生的結果所形成的集合叫做樣本空間,以S表示。樣本空間中的每一可能發生的結果,稱為一個樣本,樣本點的個數以n(S)表示。
2. 事件:樣本空間的每一子集為一個事件。
(1) 全事件:樣本空間S本身是自己的部分集合,稱S為全事件或必然事件。
(2) 空事件:部分集合Æ不含任何樣本,稱Æ為空事件或不可能事件。
(3) 基本事件:只含一個樣本點的事件稱為基本事件。
(4) 餘事件:樣本空間S中不包含A的部分集合(叫做A的補集,以A¢表示),稱A¢為A的餘事件。
(5) 和事件:A和B兩事件至少有一事件發生的事件,以AÈB表示。
(6) 積事件:A和B兩事件同時發生的事件,以AÇB表示。
(7) 互斥事件:若AÇB = Æ,則稱A和B兩事件為互斥事件。
1. 古典機率:
設一隨機試驗的樣本空間S中的各基本事件出現的機會均等。若AÌS為一事件,則事件A發生的機率為A的元素個數n(A)與S的元素個數n(S)之比,記為

2. 機率的性質:
(1) P(Æ) = 0,即空事件的機率為0。
(2) P(S) = 1,即全事件的機率為1。
(3) 若AÌS為一事件,則0 £ P(A) £ 1。
(4) 若AÌS為一事件,A¢為A的餘事件,則P(A¢) = 1 - P(A)。
(5) 若AÌBÌS的兩事件,則P(A) £ P(B)。
(6) 若A和B為S的兩事件,則P(AÈB) = P(A) + P(B) - P(AÇB)。
(7) 若A和B為S的兩事件,且A和B為互斥事件(即AÇB
=
Æ),
則P(AÈB)
=
P(A) +
P(B)。
3. 條件機率:
設A、B為樣本空間S中的兩事件,且P(A)
>
0,則在事件A發生的條件下,事件B發生的機率為

4. 獨立事件:
設A、B為樣本空間S中的任兩事件,若P(AÇB)
=
P(A) ´
P(B),則稱A、B為獨立事件,否則稱為相關事件。
5. 若A、B為獨立事件,則下列各對事件亦為獨立事件:
(1) A與B¢
(2) A¢與B
(3) A¢與B¢
數學期望值:
(1) 設某一事件發生的機率為p,該事件發生所得到的報酬為m,則稱
E = p ´ m
為此事件的數學期望值。
(2) 設一試驗有n種可能結果,其發生的機率分別為p1,p2,……,pn,各結果所得到的報酬為m1,m2,……,mn,則稱
E = p1 ´ m1 + p2 ´ m2 + …… + pn ´ mn
為此試驗的數學期望值。
1. 次數分配表的編製:
(1) 求全距。
(2) 定組數與組距。
(3) 定組限。
(4) 歸類劃記並計算各組的次數。
2. 直方圖的畫法:
以變量為橫軸,次數為縱軸,各組組距為底,其對應的次數為高,畫長方形。
3. 次數分配曲線圖的畫法:
將各組的組中點為橫坐標,其所對應的次數為縱坐標描點,依次用線段連接起來的折線。
4. 累積次數分配表的編製:
將次數分配表中各組的次數,從最小一組到最大一組累加而得「以下累積次數分配表」;從最大一組到最小一組累加而得「以上累積次數分配表」。
5. 累積次數分配曲線圖的畫法:
(1) 以各組上限為橫坐標,其所對應的以下累積次數為縱坐標描點,連接(L1,0)及各點而得。
(2) 以各組下限為橫坐標,其所對應的以上累積次數為縱坐標描點,連接(Uk,0)及各點而得。
1. 算術平均數:
(1) 未分組資料:
(2) 已分組資料: (f1
+
f2 +
……
+ fk
=
n)
(f1
+
f2 +
……
+ fk
=
n)
2. 加權平均數: (其中Wi表xi的權數)
(其中Wi表xi的權數)
3. 眾數:在一群數值資料中出現次數最多的數,以Mo表示。
4. 中位數:將n個數值從小而大排列成x1 £ x2 £ …… £ xn,
(1) 當n為奇數時,中位數![]()
(2) 當n為偶數時,中位數
5. 百分等級:
 (x為某一原始分數)
(x為某一原始分數)
1. 全距:R =最大數減去最小數
2. 四分位距:IQR = Q3 - Q1
3. 離均差:數值資料中各數值與算術平均數之差。
4. 設n個實數x1,x2,……,xn的算術平均數是![]() ,則n個實數的
,則n個實數的
(1) 母體變異數
(2) 母體標準差
(3) 樣本變異數
(4) 樣本標準差
1. 統計的意義:面對不確定的情況下,能找出事件的通則,並作出最佳的決策。
2. 抽樣方法:
(1)簡單隨機抽樣 (2)系統抽樣
(3)分層隨機抽樣 (4)部落抽樣
1. 常態分配:
由中間向兩邊對稱下降,用圓滑曲線連接,其分配曲線如鐘形一般,我們稱此資料的分配為常態分配,亦稱為高斯分配。
2. 常態分配曲線共同的特性:68 - 95 - 99.7規則
(1) 68%的數值落在距平均數m正負一個標準差的範圍內,即有68%的資料介於x = m - s 和x = m + s 兩鉛直線之間。
(2) 95%的數值落在距平均數m正負兩個標準差的範圍內,即有95%的資料介於x = m - 2s 和x = m + 2s 兩鉛直線之間。
(3) 99.7%的數值落在距平均數m正負三個標準差的範圍內,即有99.7%的資料介於x = m - 3s 和x = m + 3s 兩鉛直線之間。
3. 參數: (N為投票人數,M為支持者的人數)。
(N為投票人數,M為支持者的人數)。
4. 信賴區間:
估計真正的p值落在哪一個範圍,以區間
[估計值 - 抽樣誤差,估計值 + 抽樣誤差]
表示。
5. 信心水準:落在信賴區間的機率稱之。
1. 圓的標準式:
圓心為(h,k),半徑為r的圓方程式為(x
-
h)2 +
(y -
k)2 =
r2。
2. 圓的一般式:
凡是圓皆可表為二元二次方程式x2
+
y2 +
dx +
ey +
f =
0。一個二元二次方程式x2
+
y2 +
dx +
ey +
f =
0的圖形,依d2
+
e2 -
4f之值的不同,可得下列三種情形:
(1) 當d2
+
e2 -
4f >
0時:x2
+
y2 +
dx +
ey +
f =
0表一圓,
圓心為 ,半徑
,半徑 。
。
(2) 當d2
+
e2 -
4f =
0時:x2
+
y2 +
dx +
ey +
f =
0表一點 。
。
(3) 當d2 + e2 - 4f < 0時:x2 + y2 + dx + ey + f = 0沒有圖形。
我們將d2 + e2 - 4f稱為圓的判別式。
1. 圓與直線的關係:
圓C:(x
-
h)2 +
(y -
k)2 =
r2與直線L:ax
+
by +
c =
0的關係有三種情形:
(1) 圓與直線相交於兩點(相割),此時d
<
r,且直線L被圓C所截得的弦長為![]() 。
。
(2) 圓與直線相交於一點(相切),此時d = r。
(3) 圓與直線無交點(相離),此時d
>
r,其圓上點到直線的最近距離為
d -
r,最遠距離為d
+
r。
其中d為圓心A(h,k)到直線L:ax + by + c = 0之距離,即
 。
。
2. 圓與點的關係:
設圓心A(h,k),平面上一點P(x0,y0)與圓(x
-
h)2 +
(y -
k)2 =
r2(或x2
+
y2 +
dx +
ey +
f =
0)的關係有三種:
(1) 若P為圓內點,此時![]()
則(x0
-
h)2 +
(y0 -
k)2 <
r2(或x02
+
y02
+ dx0
+
ey0 + f
< 0)
(2) 若P為圓上點,此時![]()
則(x0
-
h)2 +
(y0 -
k)2 =
r2(或x02
+
y02
+ dx0
+
ey0 + f
= 0)
(3) 若P為圓外點,此時![]()
則(x0
-
h)2 +
(y0 -
k)2 >
r2(或x02
+
y02
+ dx0
+
ey0 + f
> 0)
3. 圓的切線:
平面上有一圓(x
-
h)2 +
(y -
k)2 =
r2與一點P(x0,y0)
(1) 過圓上一點P(x0,y0)的切線只有一條,利用切線垂直過切點的半徑求之。
(2) 過圓外一點P(x0,y0)的切線必有二條,利用圓心到切線距離等於圓的半徑求之。
【註】過圓外點的切線必有兩條,若求出切線斜率m,只有一個解,則
另一切線的斜率不存在,此切線為鉛直線。
(3) 已知切線斜率求切線,利用圓心到切線的距離等於圓的半徑求之。
4. 圓的切線段長:
從圓外一點P(x0,y0)到圓的切線段長
(1) 若圓方程式為標準式(x - h)2 + (y - k)2 = r2,則切線段長為
![]()
(2) 若圓方程式為一般式x2 + y2 + dx + ey + f = 0,則切線段長為
![]()
1. 圓錐曲線:
圓、拋物線、橢圓與雙曲線合稱為圓錐曲線,簡稱為錐線。用一個平面以不同角度切割圓錐,可以得到不同的圓錐曲線:拋物線、橢圓、雙曲線。
2. 拋物線的定義:
在平面上,設有一定直線L與L外一定點F,所有到L的距離等於到F的距離之動點P所形成的圖形稱為拋物線。也就是滿足
![]() (d(P,L)表動點P到直線L的距離)
(d(P,L)表動點P到直線L的距離)
之P點所成的集合,其中定直線L稱為準線,定點F稱為焦點。
3. 拋物線的標準式:
|
y2 = 4cx |
x2 = 4cy |
|
?若c > 0,開口向右; 若c < 0,開口向左 ?頂點:(0,0) ?焦點:F(c,0) ?準線:x = - c ?軸:y = 0 ?正焦弦長:4| c | |
?若c > 0,開口向上; 若c < 0,開口向下 ?頂點:(0,0) ?焦點:F(0,c) ?準線:y = - c ?軸:x = 0 ?正焦弦長:4| c | |
4. 拋物線的標準式的平移:
|
(y - k)2 = 4c(x - h) |
(x - h)2 = 4c(y - k) |
|
?若c > 0,開口向右; 若c < 0,開口向左 ?頂點:(h,k) ?焦點:(h + c,k) ?準線:x = h - c ?軸:y = k ?正焦弦長:4| c | |
?若c > 0,開口向上; 若c < 0,開口向下 ?頂點:(h,k) ?焦點:(h,k + c) ?準線:y = k - c ?軸:x = h ?正焦弦長:4| c | |
1. 橢圓的定義:
平面上與兩定點F1、F2距離和為定值2a(![]() )的所有點P所成的圖形稱為橢圓。也就是滿足
)的所有點P所成的圖形稱為橢圓。也就是滿足![]() 之P點所成的集合,其中兩定點F1與F2稱為橢圓的焦點。
之P點所成的集合,其中兩定點F1與F2稱為橢圓的焦點。
2. 橢圓的標準式:
|
長軸在x軸上 (a > b > 0,a2 = b2 + c2) |
長軸在y軸上 (a > b > 0,a2 = b2 + c2) |
|
?中心:(0,0) ?焦點:( ± c,0) ?長軸長:2a,長軸頂點:( ± a,0) 短軸長:2b,短軸頂點:(0, ± b)
?正焦弦長: |
?中心:(0,0) ?焦點:(0, ± c) ?長軸長:2a,長軸頂點:(0, ± a) 短軸長:2b,短軸頂點:( ± b,0)
?正焦弦長: |
3. 橢圓的標準式的平移:
|
長軸平行x軸 (a > b > 0,a2 = b2 + c2) |
長軸平行y軸 (a > b > 0,a2 = b2 + c2) |
|
?中心:(h,k) ?焦點:(h ± c,k) ?長軸長:2a,長軸頂點:(h ± a,k) 短軸長:2b,短軸頂點:(h,k ± b)
?正焦弦長: |
?中心:(h,k) ?焦點:(h,k ± c) ?長軸長:2a,長軸頂點:(h,k ± a) 短軸長:2b,短軸頂點:(h ± b,k)
?正焦弦長: |
1. 雙曲線的定義:
設F1與F2為平面上滿足![]() (c
>
0)的兩定點,平面上與兩定點F1、F2距離差的絕對值為定值2a(
(c
>
0)的兩定點,平面上與兩定點F1、F2距離差的絕對值為定值2a(![]() )的所有點P所成的圖形稱為雙曲線。也就是滿足
)的所有點P所成的圖形稱為雙曲線。也就是滿足![]() 之P點所成的集合,其中兩定點F1與F2稱為雙曲線的焦點。
之P點所成的集合,其中兩定點F1與F2稱為雙曲線的焦點。
2. 雙曲線的標準式:
|
貫軸在x軸上 (c2 = a2 + b2) |
貫軸在y軸上 (c2 = a2 + b2) |
|
?中心:(0,0) ?貫軸長:2a,頂點:( ± a,0) ?共軛軸長:2b, 共軛軸頂點:(0, ± b) ?焦點:( ± c,0),其中c2 = a2 + b2
?正焦弦長:
?漸近線: |
?中心:(0,0) ?貫軸長:2a,頂點:(0, ± a) ?共軛軸長:2b, 共軛軸頂點:( ± b,0) ?焦點:(0, ± c),其中c2 = a2 + b2
?正焦弦長:
?漸近線: |
3. 雙曲線的標準式的平移:
|
貫軸平行x軸 (c2 = a2 + b2) |
貫軸平行y軸 (c2 = a2 + b2) |
|
?中心:(h,k) ?貫軸長:2a,貫軸頂點:(h ± a,k) ?共軛軸長:2b, 共軛軸頂點:(h,k ± b) ?焦點:(h ± c,k)
?正焦弦長:
?漸近線: |
?中心:(h,k) ?貫軸長:2a,貫軸頂點:(h,k ± a) ?共軛軸長:2b, 共軛軸頂點:(h ± b,k) ?焦點:(h,k ± c)
?正焦弦長:
?漸近線: |
1. 函數:
設x、y為兩變數,給定x值後,y值隨著x值依某種關係而確定,我們稱y為x的函數,其變量x稱為自變數,變量y稱為應變數。自變數x可能變動的範圍,稱為此函數的定義域,與x值對應之函數值所成的集合稱為值域。
2. 函數極限的定義:
當函數f
(x)定義域中的x趨近於定值a時(x
¹
a),則x所對應的函數值f
(x)也逐漸趨近於a,我們稱x趨近於a時,f
(x)的極限為a,記為![]() 。
。
3. 求極限值![]() :
:
(1) 若以x
=
a代入f
(x)得實數f
(a),則![]() 。
。
(2) 若f
(x)為有理函數且 (q(x)
¹
0):
(q(x)
¹
0):
?以x
=
a代入f
(x)得![]() (無意義),此時須將f
(x)中使分子和分母為0
(無意義),此時須將f
(x)中使分子和分母為0
的公因式約去,再將x
=
a代入求得極限值。
?以x
=
a代入f
(x)得![]() (k為任意不為0之數),則
(k為任意不為0之數),則![]() 不存在。
不存在。
4. 函數極限的運算性質:
設![]() ,
,![]() ,其中a、b
皆為實數,則:
,其中a、b
皆為實數,則:
(1) ![]() (k為常數)
(k為常數)
(2) ![]() (k為常數)
(k為常數)
(3) ![]()
(4) ![]()
(5)  (b
¹
0)
(b
¹
0)
5. 極限值存在:
左極限
=
右極限,即![]() 。
。
6. 函數的連續性:
若函數f
(x)滿足(1)f
(a)存在 (2)![]() 存在 (3)
存在 (3)![]()
則稱函數f
(x)在x
=
a連續。
1. 導數的定義:
設f
(x)為一函數,a為定義域中的一點,則:
(1) f (x)在區間[a,b]的平均變化率為
(2) 若 存在,我們稱極限值
存在,我們稱極限值 為f
(x)在x
=
a的導數,以f
¢(a)表示之,即
為f
(x)在x
=
a的導數,以f
¢(a)表示之,即
 (h
=
x -
a)
(h
=
x -
a)
2. 導數的意義:
(1) 幾何意義:f ¢(a)為f (x)在x = a的切線斜率,過曲線f (x)上一點(a,f (a))的切線方程式為y - f (a) = f ¢(a)(x - a)。
(2) 物理意義:設運動物體的位移函數為f (t),速度函數為v(t),加速度函數為a(t),則f ¢(t) = v(t),v¢(t) = a(t)。
3. 導函數:
設f
(x)定義中的每一點a,其導數f
¢(a)存在,此時a→f
¢(a)形成一個新函數,f
(x)的導函數為 ,此過程稱為將函數f
(x)微分。
,此過程稱為將函數f
(x)微分。
4. 函數的可微與連續關係:可微分函數必為連續函數;反之,未必成立。
1. 微分公式:
設p(x)和q(x)皆為可微分函數,
(1) 若f (x) = xr,則f ¢(x) = rxr - 1(r為實數)
(2) 若f (x) = k,則f ¢(x) = 0(k為常數)
(3) 若f (x) = kp(x),則f ¢(x) = kp¢(x)(k為常數)
(4) 若f (x) = p(x) ± q(x),則f ¢(x) = p¢(x) ± q¢(x)
(5) 若f (x) = p(x)q(x),則f ¢(x) = p¢(x)q(x) + p(x)q¢(x)
(6) 若 且q(x)
¹
0,則
且q(x)
¹
0,則
(7) 連鎖規則:
?f
(x) =
p(q(x))且p¢(x)、q¢(x)皆存在,則f
¢(x)
=
p¢(q(x))
´
q¢(x)
?已知g(x)為可微分函數,若f
(x) =
(g(x))r且r為實數,則
f ¢(x) = r(g(x))r - 1 ´ g¢(x)
2. 高階導函數:
f (x)的n階導函數,記為
f (n)(x), ,y(n),
,y(n),![]() ,
,
f (x)的二階以上的導函數,統稱為高階導函數。
1. 函數的遞增與遞減:函數f (x)在區間I可微分,對於任意xÎI,
(1) 若f ¢(x) ³ 0,則f (x)在區間I上為遞增函數。
(2) 若f ¢(x) > 0,則f (x)在區間I上為嚴格遞增函數。
(3) 若f ¢(x) £ 0,則f (x)在區間I上為遞減函數。
(4) 若f ¢(x) < 0,則f (x)在區間I上為嚴格遞減函數。
2. 導數與極值的關係:
若函數f
(x)在x
=
a處有極大值或極小值,且f
(x)在x
=
a處可微分,則
f ¢(a)
=
0。
3. 函數的極大值與極小值:
設函數f
(x)在x
=
a附近各點都可微分且f
¢(a)
=
0,
(1) 當圖形在a點的左側是遞增函數,在a點的右側是遞減函數,即x < a時f ¢(x) > 0,x > a時f ¢(x) < 0,則f (x)在x = a處有極大值f (a)。
(2) 當圖形在a點的左側是遞減函數,在a點的右側是遞增函數,即x < a時f ¢(x) < 0,x > a時f ¢(x) > 0,則f (x)在x = a處有極小值f (a)。
4. 函數的最大值與最小值:
函數在區間範圍內的最大值與最小值,可能發生在f
¢(x)
=
0的點或區間的兩端點。
5. 極值的應用:利用多項函數求極值的方法解決一些實際的問題。
1. 無窮數列的極限:
(1) 無窮數列áanñ,當n→¥時,an→A(定值),即áanñ收斂於A,記為![]() 。
。
(2) 無窮數列áanñ沒有收斂,即為發散。
2. 無窮收斂數列的性質:
設![]() ,
,![]() ,則
,則
(1) ![]()
(2) ![]()
(3) ![]()
(4)  (B
¹
0)
(B
¹
0)
(5) ![]() (c為一常數)
(c為一常數)
3. 分式型數列極限的規則:
(1) 若an的分子和分母同次方,則![]() 即為分子分母最高次項的係數比值。
即為分子分母最高次項的係數比值。
(2) 若an的分子次方小於分母次方,則![]() 。
。
(3) 若an的分子次方大於分母次方,則![]() 不存在。
不存在。
4. 夾擠定理:
若數列áanñ,ábnñ,ácnñ滿足an
£
bn £
cn(n為任意自然數),且![]() ,則
,則![]() 。
。
5. 無窮等比數列árnñ的收斂與發散:
(1) 當
- 1
<
r <
1(即| r
| <
1)時,árnñ收斂於0;
當r
=
1時,árnñ收斂於1。
故當
- 1
<
r £
1時,árnñ為收斂數列。
(2) 當r £ - 1或r > 1時,árnñ為發散數列。
6. 無窮等比級數的收斂與發散:
(1) 當
- 1
<
r <
1(即| r
| <
1)時, 收斂,其和為
收斂,其和為![]() 。
。
(2) 當r
£
-
1或r
³
1時, 發散,級數和不存在。
發散,級數和不存在。
1. 定積分:
函數f
(x)在閉區間[a,b]上的定積分,以![]() 表示之,a與b分別稱為積分的下限與上限。
表示之,a與b分別稱為積分的下限與上限。
2. 反導函數:
設F(x)為一可微分函數,f
(x)為一函數,若F¢(x)
=
f (x),則稱F(x)為f
(x)的反導函數。
3. 不定積分的性質:
若![]() 與
與![]() 存在,其中
存在,其中![]() ,c為常數,則:
,c為常數,則:
(1) ![]()
(2)  (n
¹
-
1)
(n
¹
-
1)
(3) ![]()
(4) ![]()
4. 代換積分法:
 ,其中n
¹
-
1
,其中n
¹
-
1
1. 微積分基本定理:
設f
(x)在[a,b]上連續,且F(x)為f
(x)的反導函數,則
![]() 。
。
2. 定積分的性質:
設f
(x),g(x)均為[a,b]上可積分函數,![]()
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]() ,其中a
<
c <
b
,其中a
<
c <
b
(5) ![]()
1. 在數線上,兩點P(a)、Q(b)間的距離為
![]()
2. 坐標平面上兩點P(x1,y1)、Q(x2,y2)間的距離為
![]()
▲祕訣

3.
設P1(x1,y2)、P2(x2,y2)、P(x,y)是一直線上相異三點,且P是![]()
的內分點,若![]() (m、n為正數),則
(m、n為正數),則
 ,
,
4. 若P1(x1,y1)、P2(x2,y2)為平面上任兩點,則![]() 的中點坐標是
的中點坐標是

5. 在△ABC中,若A(x1,y1)、B(x2,y2)、C(x3,y3)且G(x,y)為△ABC的重心,則 ,
,
1. 斜率的定義:
設P1(x1,y1)、P2(x2,y2)為直線L上之相異兩點
(1) 若L不垂直於x軸,則L之斜率為

(2) 若L垂直於x軸,則L之斜率不存在
2. 已知兩直線L1、L2之斜率分別為m1、m2,則
(1) L1//L2 Û m1 = m2
(2) 若m1m2 ¹ 0,則L1 ^ L2 Û m1 ´ m2 = - 1
3. 直線方程式的型式
型一:點斜率:過點(x1,y1)且斜率為m之直線方程式為
y - y1 = m(x - x1)
型二:斜截式:若直線L的斜率為m且y截距為b,則L之方程式為
y = mx + b
型三:兩點式:若P1(x1,y1)、P2(x2,y2)為直線L上之相異兩點
(1)當x1 ¹ x2,則直線L之方程式為

(2)當x1 = x2,則直線L之方程式為
x = x1
型四:截距式:若直線L的x截距為a,y截距為b,ab ¹ 0,則L之方程式為

型五:一般式:直線L的一般式為二元一次方程式ax + by + c = 0
(1)當b = 0,表垂直x軸之直線,斜率不存在
(2)當b
¹
0,表斜率為![]() 的直線
的直線
4. 點P(x0,y0)到直線L:ax
+
by +
c =
0之距離為
5. 兩平行線L1:ax
+
by +
c1 =
0與L2:ax
+
by +
c2 =
0的距離為
 。
。
1. 兩個變數x、y,對於每一個x值已知時,就有一個且只有一個y值與之對應,則稱y為x的函數,以y = f (x)表示。其中x稱為自變數,y稱為應變數。
2. 凡能化成y = ax + b型式(式中a、b為常數)的函數,皆稱為線型函數。若a ¹ 0時,則稱為一次函數,其圖形為一直線。
3. 二次函數y
=
ax2 +
bx +
c的圖形為拋物線,
a >
0時,拋物線開口向上;
a <
0時,拋物線開口向下。
且其頂點坐標為 ,其對稱軸為
,其對稱軸為 。
。
1. 角的度量有「六十分制」與「弧度制」二種。
(1)  (弧度)
(弧度)
(2) 1(弧度)
2. 若一個扇形的半徑為r,弧長為S,所對的圓心角為q 弧度,面積為A,則
(1) S = rq
(2) 
3. 認識同界角與標準位置角
(1) 若q - f = n ´ 360°或q - f = 2np,其中n為整數,則稱q 與f 為同界角。
(2)
第一象限角:若0°
<
q
<
90°,n為整數,則n
´
360°
+
q
為第一象限角。
第二象限角:若90°
<
q
<
180°,n為整數,則n
´
360°
+
q
為第二象限角。
第三象限角:若180°
<
q
<
270°,n為整數,則n
´
360°
+
q
為第三象限角。
第四象限角:若270°
<
q
<
360°,n為整數,則n
´
360°
+
q
為第四象限角。
▲圖2-28

1.
銳角三角函數的定義:
直角△ABC中(如右圖)






2. 了解餘角關係式:
sin(90°
-
q
)
= cosq
cos(90°
-
q
)
= sinq
tan(90°
-
q
)
= cotq
cot(90°
-
q
)
= tanq
sec(90°
-
q
)
= cscq
csc(90°
-
q
)
= secq
3. 熟記特別角之三角函數值:
|
函數值 角度q |
sinq |
cosq |
tanq |
cotq |
secq |
cscq |
|
|
|
|
|
|
|
2 |
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
2 |
|
4. 熟悉基本三角關係式:
(1) 倒數關係:sinq ´ cscq = cosq ´ secq = tanq ´ cotq = 1
(2)
商數關係:

(3) 平方關係:sin2q + cos2q = 1 1 + tan2q = sec2q 1 + cot2q = csc2q
1. 在標準位置角q
之終邊上任一點P(x,y),設![]() ,則
,則


 (x
¹
0)
(x
¹
0)
 (y
¹
0)
(y
¹
0)
 (x
¹
0)
(x
¹
0)
 (y
¹
0)
(y
¹
0)
2. 由定義知同界角之三角函數值相等。
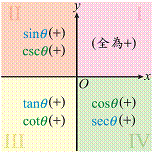
▲圖2-29

3. 由q 之終邊所在象限可確定其三角函數值正負如下:
|
正負 函數 |
一 |
二 |
三 |
四 |
|
sinq cscq |
+ |
+ |
- |
- |
|
cosq secq |
+ |
- |
- |
+ |
|
tanq cotq |
+ |
- |
+ |
- |
4. 熟記0°、90°、180°、270°之三角函數值:
|
函數值 函數 |
0°(0) |
|
180°(p ) |
|
|
sinq |
0 |
1 |
0 |
- 1 |
|
cosq |
1 |
0 |
- 1 |
0 |
|
tanq |
0 |
無意義 |
0 |
無意義 |
5. 第一類三角函數變換公式:
(1) sin( - q ) = - sinq cos( - q ) = cosq tan( - q ) = - tanq
(2) sin(p - q ) = sinq cos(p - q ) = - cosq tan(p - q ) = - tanq
(3) sin(p + q ) = - sinq cos(p + q ) = - cosq tan(p + q ) = tanq
(4) sin(2p - q ) = - sinq cos(2p - q ) = cosq tan(2p - q ) = - tanq
6. 第二類三角函數變換公式:
(1) 


(2) 


(3) 


1. 函數y = sinx的性質:
(1) x為任意實數,sinx均有意義
(2) - 1 £ sinx £ 1
(3) 週期為2p
2. 函數y = cosx的性質:
(1) x為任意實數,cosx均有意義
(2) - 1 £ cosx £ 1
(3) 週期為2p
3. 函數y = tanx的性質:
(1) 直線 (n為整數)為圖形之漸近線
(n為整數)為圖形之漸近線
(2) tanx可為任意實數
(3) 週期為p
4. 函數y = cotx的性質:
(1) x = np(n為整數)為圖形之漸近線
(2) cotx可為任意實數
(3) 週期為p
5. 函數y = secx的性質:
(1)  (n為整數)為圖形之漸近線
(n為整數)為圖形之漸近線
(2) | secx | ³ 1
(3) 週期為2p
6. 函數y = cscx的性質:
(1) x = np(n為整數)為圖形之漸近線
(2) | cscx | ³ 1
(3) 週期為2p
1. 有向線段與向量:對於每一個向量![]() 均有一個有向線段
均有一個有向線段![]() 與之對應,記為
與之對應,記為![]() 。
。
2. 向量的坐標表示:
(1) 設O為原點,點P(a,b),則![]() 且
且![]()
(2) 設A(a1,a2)、B(b1,b2),則![]()
3. 向量的相等:
設![]() 、
、![]() ,若
,若![]() ,則a1
=
b1且a2
=
b2
,則a1
=
b1且a2
=
b2
1. 向量的加減法:
在△ABC中
(1) ![]()
(2) ![]()
2. 向量加減法的坐標表示:
設![]() 、
、![]() ,則
,則
(1) ![]()
(2) ![]()
3. 向量加法的基本性質:
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]() ,稱
,稱![]() 為
為![]() 的逆向量
的逆向量
4. 向量的實數積:
設r為實數,則![]() 稱為向量的實數積,若
稱為向量的實數積,若![]() ,則
,則
(1) r
> 0時,![]() 與
與![]() 同向,且長度為
同向,且長度為![]() 的r倍。
的r倍。
(2) r
< 0時,![]() 與
與![]() 反向,且長度為
反向,且長度為![]() 的|
r |倍。
的|
r |倍。
5. 向量實數積的坐標表示:
設![]() ,r為實數,則
,r為實數,則![]()
6. 向量實數積的基本性質:
r、s為實數,則
(1) ![]()
(2) ![]() ;
;![]()
7. 向量的平行:
![]() ,
,![]()
(1) 若![]() ,則存在一實數r,使得
,則存在一實數r,使得![]()
(2) 設![]() ,
,![]() ,若
,若![]() ,則a1:b1
=
a2:b2
,則a1:b1
=
a2:b2
8. 長度為1的向量,稱為單位向量,即若(x,y)為一個單位向量,則x2
+
y2 =
1,若![]() 為非零向量,則與
為非零向量,則與![]() 同向的單位向量為
同向的單位向量為![]() 。
。
1. 餘弦定理:
△ABC中,若a、b、c分別表示ÐA、ÐB、ÐC的對邊,則
a2 =
b2 +
c2 -
2bccosA
b2 =
a2 +
c2 -
2accosB
c2 =
a2 +
b2 -
2abcosC
2. 向量的內積:
(1) 設q
為![]() 與
與![]() 的夾角,則
的夾角,則![]() 、
、![]() 的內積為
的內積為![]()
(2) 設![]() 、
、![]() ,則
,則![]()
3. 向量的垂直:
設![]() ,
,![]() ,若
,若![]() ,則
,則![]()
4. 向量內積的性質:
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
1. 指數的定義:
設n為正整數,則符號an表示n個a的連乘積。
2. 整數指數:
設a
¹
0,n為正整數,則
(1) a0 = 1
(2) 
3. 分數指數:
若a為正實數,且m、n為整數,n
>
0,則
(1) ![]()
(2) ![]()
4. 實數指數的指數律:
設a、b為正實數,r、s為實數,則
(1) ar ´ as = ar + s
(2) (ar)s = ars
(3) ar ´ br = (ab)r
(4) 
(5) 
1. 指數函數:
設a
>
0且a
¹
1,若將任意實數x視為一變數,則函數y
=
f (x) =
ax稱為以a為底數的指數函數。
2. 指數函數圖形的性質:
(1) 圖形恆在x軸的上方,且漸漸接近於x軸。
(2) 圖形通過點(0,1)。
(3) 當a > 1時,y = ax為嚴格增函數。
(4) 當0 < a < 1時,y = ax為嚴格減函數。
(5) 設a
>
0且a
¹
1,則y
=
ax與 的圖形對稱於y軸。
的圖形對稱於y軸。
3. 指數方程式:
(1) 方程式中的未知數出現在指數部分者,稱為指數方程式。
(2) 求解原理:若a > 0、a ¹ 1且ar = as,則r = s。
1. 對數的定義:
設a
>
0且a
¹
1,b
>
0,則滿足ax
=
b的唯一實數x,稱為以a為底數之b的對數,記為logab
=
x,且稱b為真數。
2. 對數的性質:
設a、b、M、N均為正實數,且a、b
¹
1;r、s為實數,且r
¹
0,則
(1) loga1 = 0;logaa = 1
(2) loga(MN) = logaM + logaN
(3)  ;
;
(4)  ;
;
(5)  (換底公式);(logab)
´
(logba)
= 1
(換底公式);(logab)
´
(logba)
= 1
1. 對數函數:
設a
>
0且a
¹
1、x
>
0,若將x視為一變數,則函數y
=
f (x) =
logax稱為以a為底數的對數函數。
2. 對數函數圖形的性質:
(1) 圖形恆在y軸的右側,且漸漸接近於y軸。
(2) 圖形通過點(1,0)。
(3) 當a > 1時,y = logax為嚴格增函數。
(4) 當0 < a < 1時,y = logax為嚴格減函數。
(5) 設a
>
0且a
¹
1,則y
=
logax與![]() 的圖形對稱於x軸。
的圖形對稱於x軸。
(6) 設a > 0且a ¹ 1,則y = ax與y = logax的圖形對稱於直線y = x。
3. 對數方程式:
(1) 方程式中的未知數出現在對數中的真數或底數者,通稱為對數方程式。
(2) 求解原理:若a > 0且a ¹ 1,M、N > 0且logaM = logaN,則M = N。
1. 常用對數:
以10為底數的對數,稱為常用對數,簡記為logx。
2. 熟知常用對數表的查法及表尾差法的使用。
3. 首數、尾數:
若logx
=
n +
a,其中n為整數,0
£
a
<
1,則稱n為首數,a
為尾數。
(1) 若x > 1,且x的整數部分為m位數,則n = m - 1。
(2) 若0 < x < 1,且x自小數點後第m位開始出現不為0的數字,則n = - m。
1. 等差數列的第k項
ak
=
a1 +
(k -
1) ´
d
2. 等差級數前n項的和

3. 等差中項A為前後二項a、b和的一半,即

1. 等比數列的第k項
ak
=
a1 ´
rk
- 1
2. 等比級數的前n項和
 (r
¹
1)
(r
¹
1)
3. 等比中項G的平方等於前後二項a、b的乘積,即
G2
=
a ´
b(或![]() )
)
1. 無窮數列áanñ,
當n→¥時,an→a,則稱a
為數列áanñ之極限,記為![]() 。
。
又「極限存在」的數列稱為收斂數列;
「極限不存在」的數列,稱為發散數列。
2. 無窮等比數列áarn - 1ñ,r ¹ 0中
(1) 當| r | < 1或r = 1時,數列áarn - 1ñ為收斂數列。
(2) 當| r | > 1或r = - 1時,數列áarn - 1ñ為發散數列。
3. 無窮級數![]() ,前n項和
,前n項和 ,
,
(1) 若![]() ,則稱
,則稱![]() 為收斂級數,且其和為a。
為收斂級數,且其和為a。
(2)
若![]() 不存在,則稱
不存在,則稱![]() 為發散級數,且其和不存在。
為發散級數,且其和不存在。
4. 無窮等比級數 (a
¹
0,r
¹
0),
(a
¹
0,r
¹
0),
(1) 若|
r | <
1,則 為收斂級數,且其和為
為收斂級數,且其和為![]() 。
。
(2) 若|
r | ³
1,則 為發散級數,且其和不存在。
為發散級數,且其和不存在。
1. 多項式的相等:兩多項式的次數相同,且對應項的係數相等。
2. 多項式的相加減運算:只要將同類項的係數相加減即可。
3. 多項式的乘法及除法運算:利用分離係數法較容易。
4. 多項式的除法定理:
被除式 = 除式 ´ 商式 + 餘式
但其中餘式的次數要小於除式的次數,或餘式為0。
5. 綜合除法的運算:在運算中,上、下兩列的係數是用相加,不是相減。
1. 餘式定理:設a
¹
0,多項式f
(x)除以ax
-
b的餘式為![]() 。
。
2. 因式定理:設a
¹
0,若ax
-
b | f (x),則 ;反之亦成立。
;反之亦成立。
3. 因式分解公式:
(1) a2
+ 2ab
+
b2 =
(a +
b)2
a2 -
2ab +
b2 =
(a -
b)2
(2) a2 - b2 = (a + b)(a - b)
(3) a3
+ b3
=
(a +
b)(a2
- ab
+
b2)
a3 -
b3 =
(a -
b)(a2
+ ab
+
b2)
(4) a3
+ 3a2b
+
3ab2 +
b3 =
(a +
b)3
a3 -
3a2b
+ 3ab2
-
b3 =
(a -
b)3
4. 最高公因式與最低公倍式
兩個多項式f
(x)與g(x)的共同因式中,次數最高的稱為它們的最高公因式,簡記為H.C.F。又共同倍式中,次數最低的稱為它們的最低公倍式,簡記為L.C.M。
1. 分式有三種類型:
(1) 真分式:分子次數小於分母次數的分式。
(2) 假分式:分子次數不小於分母次數的分式。
(3) 帶分式:一個多項式與真分式的代數和。
2. 分式的四則運算:若f (x)、g(x)、h(x)、k(x)均為多項式且g(x)、k(x)不為零多項式,則
(1) 加法:
(2) 減法:
(3) 乘法:
(4) 除法: (其中h(x)
¹
0)
(其中h(x)
¹
0)
3. 部分分式:將一個真分式化為若干個真分式的代數和,稱為將真分式分解成部分分式。
4. 根式的性質:若A、B均為有理式,且其值皆為正數,m、n皆為正整數,則
(1) ![]()
(2) ![]()
(3) ![]()
(4) 
5. 有理化因式:若兩個根式的乘積是有理式,則稱這兩個根式互為有理化因式。
6. 二重根式的化簡:
若x
=
a +
b,y
=
ab且a
³
b >
0,則![]() 。
。
1. 一元二次方程式ax2 + bx + c = 0:
(1) b2 - 4ac > 0:有兩相異實根,可利用十字交乘法或代入公式求解。
(2) b2
- 4ac
=
0:有兩相等實根, (重根)。
(重根)。
(3) b2 - 4ac < 0:無實根。
2. 根與係數的關係:
若a、b
為一元二次方程式ax2
+
bx
+
c
=
0之兩根,則
 、
、 。
。
3. 一次因式檢驗定理:
設f
(x) =
anxn
+ an
-
1xn
-
1
+
…
+ a1x
+
a0為一個整係數n次多項式,若整係數一次式ax
-
b是f
(x)的因式,且a、b互質,則a
| an且b
| a0。
4. 一元高次方程式的解法:
可利用一次因式檢驗定理或因式分解公式,將其分解為一次或二次因式的乘積,即可求出其解。
1. 聯立方程式 解的幾何意義:
解的幾何意義:
(1) 若a1:a2 ¹ b1:b2,則聯立方程式恰有一組解(x0,y0),表此聯立方程式所對應的兩直線恰交於一點(x0,y0)。
(2) 若a1:a2 = b1:b2 = c1:c2,則聯立方程式有無限多組解,表此聯立方程式所對應的兩直線重合。
(3) 若a1:a2 = b1:b2 ¹ c1:c2,則聯立方程式無解,表此聯立方程式所對應的兩直線平行。
2. 二階行列式:
符號 表示ad
-
bc,且稱此符號為二階行列式。
表示ad
-
bc,且稱此符號為二階行列式。
3. 二元一次方程組的行列式解:
方程組 中
中
令 ,
, ,
, ,則
,則
(1) D
¹
0,方程組恰有一組解: ,
, 。
。
(2) D = 0,但Dx ¹ 0或Dy ¹ 0,方程組無解。
(3) D = 0且Dx = Dy = 0,方程組有無限多組解。
1. 三階行列式:
符號 表示a1b2c3
+
a2b3c1
+ a3b1c2
-
a3b2c1
- a1b3c2
-
a2b1c3,且稱此符號為三階行列式。
表示a1b2c3
+
a2b3c1
+ a3b1c2
-
a3b2c1
- a1b3c2
-
a2b1c3,且稱此符號為三階行列式。
2. 三階行列式的降階:
三階行列式的值等於它任何一行(或列)的各元與其對應的餘因式之乘積的和。
3. 行列式的性質:
(1) 行列依序互換,其值不變。
(2) 任意兩行(列)對調,其值變號。
(3) 任一行(列)可提出其公因數。
(4) 任一行(列)的元素均為0,其值為0。
(5) 任兩行(列)的元素對應相同或成比例,其值為0。
(6) 某一行(列)的元素若由兩個元所組成,則可分成兩個行列式之和。
(7) 將任一行(列)的k倍加到另一行(列),其值不變。
4. Cramer(克拉瑪)公式:
設
令 ,
,
 ,
,
當D
¹
0時,方程組恰有一組解:
 ,
, ,
,
1. 一元一次不等式的解法與圖示:
不等式ax
+
b >
0(a
¹
0)的解為
(1) 若a
>
0,則 。
。
(2) 若a
<
0,則 。
。
2. 設a > 0,一元二次方程式ax2 + bx + c = 0
(1) 當b2
-
4ac >
0時,有兩相異實根a、b,令a
<
b,則
?ax2
+
bx
+
c
>
0的解為x
>
b
或x
<
a
?ax2
+
bx
+
c
<
0的解為a
<
x
<
b
?ax2
+
bx
+
c
³
0的解為x
³
b或x
£
a
?ax2
+
bx
+
c
£
0的解為a
£
x
£
b
(2)
當b2
-
4ac =
0時,有相等實根,即a
=
b,則
?ax2
+
bx
+
c
³
0的解為任意實數
?ax2
+
bx
+
c
>
0的解為不等於a
的任意實數
?ax2
+
bx
+
c
£
0的解為x
=
a
?ax2
+
bx
+
c
<
0為無解
(3)
當b2
-
4ac <
0時,沒有實根,則
?ax2
+
bx
+
c
³
0的解為任意實數
?ax2
+
bx
+
c
>
0的解為任意實數
?ax2
+
bx
+
c
£
0為無解
?ax2
+
bx
+
c
<
0為無解
1. 算幾不等式:
設a1,a2,…,an為n個正實數,n
³
2,則
且當等號成立時,a1
=
a2 =
…
= an。
2. 柯西不等式:
設a1,a2,…,an,b1,b2,…,bn是2n個實數,則
(a12
+ a22
+
…
+ an2)(b12
+
b22
+
…
+ bn2)
³
(a1b1
+ a2b2
+
…
+ anbn)2
且當等號成立時,a1:b1
=
a2:b2
=
…
= an:bn。
1. 設a > 0,直線L表方程式ax + by + c = 0之圖形,則不等式
(1) ax + by + c > 0的圖形表直線L之右側半平面。
(2) ax + by + c ³ 0的圖形表直線L之右側半平面及直線L。
(3) ax + by + c < 0的圖形表直線L之左側半平面。
(4) ax + by + c £ 0的圖形表直線L之左側半平面及直線L。
2. 設平行於x軸的直線L表方程式y = k之圖形,則不等式
(1) y > k的圖形表直線L之上方半平面。
(2) y ³ k的圖形表直線L之上方半平面及直線L。
(3) y < k的圖形表直線L之下方半平面。
(4) y £ k的圖形表直線L之下方半平面及直線L。
3. 二元一次聯立不等式的圖形為各不等式之圖形的共同部分。
4. 線性規劃問題求解之一般步驟為
(1) 將題目資料列成簡明的表。
(2) 依題意列出限制條件,以聯立不等式表示。
(3) 圖解限制條件(聯立不等式),畫出可行解區域並求出頂點坐標。
(4) 依題意列出目標函數,通常為x、y的一次式。
(5) 求出可行解區域頂點所對應的目標函數值,檢驗其最大值或最小值。
1. 加法原理:
若完成某件事可分成k個類別,且每個類別不同時發生,而第i個類別有mi(i
=
1,2,…,k)種方法,則完成此件事的方法數共有m1
+
m2
+
…
+ mk種。
2. 乘法原理:
設完成某件事須經過k個步驟,且每個步驟互不影響,而完成第i個步驟有mi(i
=
1,2,…,k)種方法,則完成此件事的方法數共有m1
´
m2
´
…
´ mk種。
1. 設n為自然數,符號「n!」讀作「n階乘」,規定
n! =
n ´
(n -
1) ´
(n -
2) ´
…
´ 2
´
1。
2. 相異物的直線排列:
自n件相異物中,任取m件(1
£
m £
n),不許重複,其直線排列數為

當m
=
n時,上式為
![]() 。
。
3. 有相同物的直線排列:
設n件物品中,共有k類,第一類有m1件,第二類有m2件,…,第k類有mk件,且m1
+
m2
+
…
+ mk
=
n,則將此n件物品排成一列,共有 種方法。
種方法。
1. 重複排列:
自n類物品中,每類至少有m件(m
³
1),則任選m件的重複排列數為nm。
2. 環狀排列:
自n件相異物中,任取m件(m
£
n且不重複)作環狀排列,其排列數有 。
。
當m
=
n時,其排列數為 。
。
1. 不可重複的組合:
自n件相異物中,每次取m件(1
£
m £
n)為一組,其組合數為
 。
。
(1) ![]() 。
。
(2) ![]() 。
。
2. 巴斯卡定理:
若m、n為自然數且1
£
m £
n -
1,則![]() 。
。
1. 重複組合:
(1) m件相同物,全部分給n個人,每人可兼得的分法有![]() 種。
種。
(2) 方程式x1
+
x2 +
…
+ xn
=
m的非負整數解組數有![]() 組。
組。
(3) 自n類不同物品中,每類至少m個,每次取m個為一組,若各組中每類物品皆可重複選取,則在n類物品中取m件的重複組合數為![]() 種。
種。
2. 組合總數:
(1) 相異物的組合總數:自n件相異物中,每次至少取一件的組合總數為2n - 1。
(2) 不盡相異物的組合總數:n件物品中,其中m1件相同,m2件相同,…,mk件相同,且n
=
m1 + m2
+
…
+ mk,則自其中至少取一件的組合總數為
(m1 +
1)(m2 +
1)…(mk
+
1) -
1。
二項式定理:
對於任意正整數n,恆有
![]()
即 。
。
(1) 展開式中共有n + 1項。
(2) 一般項為第k
+
1項,即![]() 。
。
1. 集合的意義:集合是由一些明確而可辨認的事物所組成的群體。
2. 集合與集合的關係:
(1) 子集:若集合A中的每一個元素都是集合B的元素,則稱A是B的子集,記為AÌB。
(2) 集合相等:若AÌB且BÌA,則A = B。
3. 集合與集合的運算:
(1) 聯集:AÈB = {x | xÎA或xÎB}。
(2) 交集:AÇB = {x | xÎA且xÎB}。
(3) 差集:A - B = {x | xÎA但xÏB}。
(4) 空集合:不含任何元素的集合,記為Æ。
(5)
宇集與補集:討論一個問題時,包含問題中所有集合的固定集合,稱為宇集,記為U。屬於U,但不屬於集合A的元素所成的集合,稱為A的補集,即
A¢
=
{x | xÎU且xÏA}。
4. 樣本空間:一隨機試驗中,所有可能發生的結果所成的集合,稱為此試驗的樣本空間,以S表之。
5. 事件:樣本空間中的每一個子集,稱為事件。
(1) 全事件:即樣本空間S本身。
(2) 空事件:即Æ。
(3) 基本事件:只含一個樣本點的事件。
(4) 和事件:即AÈB。
(5) 積事件:即AÇB。
(6) 互斥事件:當AÇB = Æ,則稱A與B互斥。
1. 古典機率的定義:
設一隨機試驗的樣本空間S,若每一樣本出現的機會均等,則每一事件A發生的機率為 。
。
2. 機率的性質:
(1) P(S) = 1。
(2) P(Æ) = 0。
(3) AÌS,則0 £ P(A) £ 1。
(4) AÌS,則P(A¢) = 1 - P(A)。
(5) 設AÌS,BÌS,則P(AÈB) = P(A) + P(B) - P(AÇB)。
(6) 設AÌS,BÌS,則P(AÇB¢) = P(A) - P(AÇB)。
3. 條件機率:
(1) 定義:設A、B為樣本空間S的任二事件,且P(A) > 0,則
 。
。
(2) 條件機率的乘法公式:
P(AÇB)
=
P(A) ´
P(B | A)。
(3) 貝氏定理:
設{A1,
A2, …,
An}是樣本空間S的一個分割,B為S的任一個事件,若P(B)
>
0,P(Ai)
>
0,i
=
1,2,…,n,則
 ,
,
k =
1,2,…,n。
4. 獨立事件:
(1) 設AÌS,BÌS,若P(AÇB) = P(A) ´ P(B),則稱A、B為獨立事件(或統計無關),否則稱為相關事件。
(2) 若P(AÇB)
=
P(A) ´
P(B),則下列三式成立:
?P(AÇB¢)
=
P(A) ´
P(B¢)。
?P(A¢ÇB)
=
P(A¢)
´
P(B)。
?P(A¢ÇB¢)
=
P(A¢)
´
P(B¢)。
1. 試驗的數學期望值:
設有一試驗,其樣本空間為S且{A1,
A2, …,
Ak}為樣本空間S的一個分割,若事件Ai發生的機率為pi(i
=
1,2,…,k),且事件Ai發生可得報酬xi(i
=
1,2,…,k),則稱p1x1
+
p2x2
+
…
+ pkxk為此試驗的數學期望值。
1. 統計內容的三要素:
(1)統計資料
(2)統計方法
(3)統計原理
2. 抽樣調查的方法:
(1)簡單隨機抽樣
(2)系統抽樣
(3)分層隨機抽樣
(4)部落抽樣
1. 次數分配表的編製:
第一步:求全距
第二步:定組數
第三步:定組距
第四步:定組限
第五步:歸類並計算各組的次數
2. 直方圖的畫法:
以變量為橫軸,次數為縱軸,各組組距為底,其對應次數為高,畫長方形,可得直方圖。
3. 學習累積次數分配表的編製。
4. 學習累積次數分配曲線圖的畫法。
1. 算術平均數的求法:
(1) 未分組資料:
(2) 已分k組資料:
2. 加權平均數的求法:
 ,其中Wi表xi的權數。
,其中Wi表xi的權數。
3. 中位數的求法:
設n個數值由小而大排列成x1
£
x2 £
…
£ xn。
(1) 當n為奇數時,中位數![]() 。
。
(2) 當n為偶數時,中位數 。
。
4. 百分等級的求法:
若n表示所登錄分數的總次數,x表示某一個原始分數,Fx表示分數小於x的累積次數,則百分等級PR為 的整數部分。
的整數部分。
1. 全距:R = 最大數 - 最小數。
2. 四分位距:IQR = Q3 - Q1。
3. 母體變異數與母體標準差:
離均差平方和的算術平均數稱為母體變異數,記為s2,而其平方根稱為母體標準差,記為s。
4. 樣本變異數與樣本標準差:
樣本資料的離均差平方和除以n
-
1,稱為樣本變異數,記為S2,而其平方根稱為樣本標準差,記為S。
5. 樣本變異數與樣本標準差的求法:
設樣本資料為x1,
x2, …,
xn,其算術平均數為![]() ,
,
則 ,
,
 。
。
1. 常態分配:68 - 95 - 99規則,大約有
(1) 68%的數值落在距平均數一個標準差的範圍內。
(2) 95%的數值落在距平均數兩個標準差的範圍內。
(3) 99%的數值落在距平均數三個標準差的範圍內。
2. 學習信賴區間與信心水準的解讀。
1. 和差角公式:
(1) cos(a - b ) = cosa cosb + sina sinb
(2) cos(a + b ) = cosa cosb - sina sinb
(3) sin(a + b ) = sina cosb + cosa sinb
(4) sin(a - b ) = sina cosb - cosa sinb
(5)

(6)

2. 二倍角公式:
(1) sin2q = 2sinq cosq
(2) cos2q = cos2q - sin2q = 1 - 2sin2q = 2cos2q - 1
(3)

3. 若a、b為實數,則函數y
=
asinx +
bcosx有
最大值![]() 、最小值
、最小值![]() 。
。
1. 正弦定理:
在△ABC中,若R為△ABC之外接圓半徑,則
2. 餘弦定理:
在△ABC中,若a、b、c分別表示ÐA、ÐB、ÐC的對邊,則
a2 =
b2 + c2
-
2bccosA b2
=
a2 + c2
-
2accosB c2
=
a2 +
b2 -
2abcosC
3. 三角形面積公式:
在△ABC中,
(1) 已知二邊一夾角,則△ABC的面積為

(2) 海龍公式:
已知三邊長為a、b、c,令 ,則△ABC的面積為
,則△ABC的面積為
![]()
1. 解三角形:
(1) 已知二角一邊(A.A.S.或A.S.A.)時,可利用正弦定理求出另二邊。
(2) 已知二邊一夾角(S.A.S.)時,可由餘弦定理求出第三邊,再利用正弦定理求出另外二角。
(3) 已知三邊長(S.S.S.)時,可由餘弦定理求出未知的三個角。
(4) 已知二邊及一對角(S.S.A.)時,
?由餘弦定理可得一個一元二次方程式,則由此方程式的解,可知三角形可能有二解、
一解或無解。
?若由正弦定理,則先求出另外的角,其解亦可能為二解、一解或無解。
2. 三角測量:
(1) 認識測量用的名詞,如:仰角、俯角及方位等。
(2) 能利用作圖,將測量的問題轉化成解三角形的問題。
1. 圓的標準式:
以Q(h,k)為圓心,r(r
>
0)為半徑之圓的方程式為(x
-
h)2 +
(y -
k)2 =
r2
2. 圓的一般式:
凡是圓,必可表為x2
+
y2 +
dx +
ey +
f =
0的形式,但此種形式的方程式,其圖形有下列三種情形:
(1) 當d2
+
e2 -
4f >
0時,方程式表一圓,圓心為 ,半徑為
,半徑為 。
。
(2) 當d2
+
e2 -
4f =
0時,方程式表一點 。
。
(3) 當d2 + e2 - 4f < 0時,方程式無圖形。
3. 點與圓的相關位置:
設點P(x0,y0),圓C:x2
+
y2 +
dx +
ey +
f =
0,則
(1) x02 + y02 + dx0 + ey0 + f > 0 Û P在圓C外部。
(2) x02 + y02 + dx0 + ey0 + f = 0 Û P在圓C上。
(3) x02 + y02 + dx0 + ey0 + f < 0 Û P在圓C內部。
1. 判斷圓與直線的相交情況:
設直線L:ax
+
by +
c =
0,圓C:(x
-
h)2 +
(y -
k)2 =
r2
(1) 令d表圓心到直線L之距離,即 ,則
,則
?d
>
r Û 圓C與直線L不相交。
?d
=
r Û 圓C與直線L恰交於一點(相切)。
?d
<
r Û 圓C與直線L相交於相異兩點。
(2) 圓C與直線L的方程式聯立,消去x或y,可得一個一元二次方程式,令其判別式為D,則
?D
>
0 Û 表圓C與直線L相交於相異兩點。
?D
=
0 Û 表圓C與直線L恰交於一點(相切)。
?D
<
0 Û 表圓C與直線L不相交。
2. 學習圓的切線方程式的求法。
3. 自圓C:x2
+
y2 +
dx +
ey +
f =
0外一點P(x1,y1)到圓C的切線段長為![]() 。
。
1. 拋物線的定義:
設平面上有一定直線L及直線L外一定點F,則在此平面上到點F的距離等於到直線L的距離之所有點所成的圖形,稱為拋物線,其中定點F為焦點,定直線L為準線。
2. 頂點在(h,k)的拋物線標準式與其圖形之間的關係:
|
標準式 |
圖形 |
|
(y - k)2 = 4c(x - h) |
|
|
(x - h)2 = 4c(y - k) |
|
1. 橢圓的定義:
設F1與F2為平面上的兩相異定點,若定數![]() ,則在此平面上滿足
,則在此平面上滿足![]() 的所有點P所成的圖形,稱為橢圓,其中定點F1與F2稱為橢圓的焦點。
的所有點P所成的圖形,稱為橢圓,其中定點F1與F2稱為橢圓的焦點。
2. 中心在(h,k)的橢圓標準式與其圖形之間的關係:
|
標準式 |
圖形 |
|
(a > b > 0) (c2 = a2 - b2) |
|
|
(a > b > 0) (c2 = a2 - b2) |
|
1. 雙曲線的定義:
設F1與F2為平面上的兩相異定點,若定數![]() ,則在此平面上滿足
,則在此平面上滿足![]() 的所有點P所成的圖形,稱為雙曲線,其中定點F1與F2稱為雙曲線的焦點。
的所有點P所成的圖形,稱為雙曲線,其中定點F1與F2稱為雙曲線的焦點。
2. 中心在(h,k)的雙曲線標準式與其圖形之間的關係:
|
標準式 |
圖形 |
|
(a > 0,b > 0) (c2 = a2 + b2) |
|
|
(a > 0,b > 0) (c2 = a2 + b2) |
|
1. 數列的極限:
若an可以向某一定數a
任意靠近,只要n足夠大,則我們說:當n趨近於無限大時,an趨近於a,且稱a
為數列áanñ的極限,記為![]() 。
。
2. 無窮等比數列的斂散性:
無窮等比數列árnñ中:
(1) 當| r | < 1或r = 1時,數列árnñ為收斂數列。
(2) 當| r | > 1或r = - 1時,數列árnñ為發散數列。
3. 夾擠定理:
若áanñ、ábnñ及ácnñ為三個無窮數列,其中![]() ,且數列ácnñ滿足:從某一項起,不等式an
£
cn £
bn恆成立,則ácnñ也是收斂數列,而且
,且數列ácnñ滿足:從某一項起,不等式an
£
cn £
bn恆成立,則ácnñ也是收斂數列,而且![]() 。
。
4. 函數的極限:
當函數f
(x)定義域中的x趨近a時(包含從a的左、右方趨近,但x
¹
a),若f
(x)會趨近於某一個定數L,則稱當x趨近a時,f
(x)的極限為L,記為![]() 。
。
5. 函數的連續:
若函數f
(x)在實數系中均有定義,且滿足下列三個條件:
(1) f (a)存在;
(2) ![]() 存在;
存在;
(3) ![]() ,
,
則稱f
(x)在x
=
a處連續。
若函數f
(x)在實數系中的每一點皆連續,則稱f
(x)為連續函數。
1. 導數的定義:
設多項函數y
=
f (x)在x
=
a處及其附近有定義,若極限 存在,則稱此極限為函數f
(x)在x
=
a處的導數,記為f
¢(a),即
存在,則稱此極限為函數f
(x)在x
=
a處的導數,記為f
¢(a),即
 ,f
¢(a)表示過點(a,f
(a))的切線斜率。
,f
¢(a)表示過點(a,f
(a))的切線斜率。
2. 可微分函數:
若多項函數f
(x)在x
=
a處的導數存在,則稱f
(x)在x
=
a處可微分,否則稱f
(x)在x
=
a處不可微分。如果多項函數f
(x)在實數線上的每一點均可微分,則稱此多項函數f
(x)是一個可微分函數。
3. 導函數:
若f
(x)是一個可微分函數,即在f
(x)的定義域中的每一點a,它的導數f
¢(a)均存在,則對應關係a→f
¢(a)所形成的函數,稱為f
(x)的導函數,記為f
¢(x)。
微分公式:
1. 若f (x) = k,k為常數,則f ¢(x) = 0。
2. 若f (x) = xn,n為正整數,則f ¢(x) = nxn - 1。
3. 設c為常數,若f (x)為可微分函數且g(x) = cf (x),則g¢(x) = cf ¢(x)。
4. 若f (x)與g(x)均為可微分函數,且h(x) = f (x) + g(x),則h¢(x) = f ¢(x) + g¢(x)。
5. 若f (x)與g(x)均為可微分函數且h(x) = f (x) ´ g(x),則h¢(x) = f ¢(x) ´ g(x) + f (x) ´ g¢(x)。
6. 若n為正整數,f (x)為可微分函數,則(f (x))n的導函數為n(f (x))n - 1 ´ f ¢(x)。
1. 函數的增減:
設f
(x)為多項函數,則
(1) 在區間(a,b)內,若f ¢(x) ³ 0恆成立,則f (x)在區間[a,b]上為遞增函數。
(2) 在區間(a,b)內,若f ¢(x) £ 0恆成立,則f (x)在區間[a,b]上為遞減函數。
2. 多項函數的極值:
若f
(x)為多項函數且f
¢(c)
=
0,則
(1) 在c點附近,當x < c時,f ¢(x) > 0;當x > c時,f ¢(x) < 0,則f (x)在x = c處有極大值。
(2) 在c點附近,當x < c時,f ¢(x) < 0;當x > c時,f ¢(x) > 0,則f (x)在x = c處有極小值。
3. 多項函數圖形的凹向與反曲點:
設f
(x)為多項函數,
(1) 若f (x)在區間(a,b)上,f ²(x) > 0恆成立,則f (x)在區間(a,b)的圖形凹口向上。
(2) 若f (x)在區間(a,b)上,f ²(x) < 0恆成立,則f (x)在區間(a,b)的圖形凹口向下。
(3) 若在c點附近,x < c時f (x)圖形的凹向與x > c時f (x)圖形的凹向相反,則稱點(c,f (c))為函數f (x)圖形的一個反曲點。
1. 不定積分的公式: ,其中c為常數。
,其中c為常數。
2. 不定積分的運算性質:
(1) ![]()
(2) ![]()
(3) ![]()
3. 定義:
(1) ![]() 。
。
(2) ![]() (其中a
£
b)。
(其中a
£
b)。
4. 定積分的運算性質:
若f
(x)與g(x)為二多項函數,則
(1) ![]() ,其中k為常數。
,其中k為常數。
(2) ![]() 。
。
(3) ![]() 。
。
5. 定積分與面積:
定積分![]() 的幾何意義是表示:y
=
f (x)的圖形與x軸及兩直線x
=
a,x
=
b所圍成的區域中,在x軸上方的面積減去在x軸下方的面積。
的幾何意義是表示:y
=
f (x)的圖形與x軸及兩直線x
=
a,x
=
b所圍成的區域中,在x軸上方的面積減去在x軸下方的面積。
1. 微積分基本定理:
若f
(x)為可微分函數,F(x)為f
(x)的一個反導函數,則
![]() 。
。
2. 兩曲線間的面積:
設二多項函數f
(x)與g(x)在區間[a,b]上,f
(x) ³
g(x)恆成立,則由y
=
f (x)的圖形與y
=
g(x)的圖形及直線x
=
a,x
=
b所圍成區域的面積為![]() 。
。
※感謝龍騰文化提供